题目内容
设F1、F2为椭圆![]() 的两个焦点,P为上一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求
的两个焦点,P为上一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求![]() 的值.
的值.
由已知,|PF1|>|PF2|,|PF1|+|PF2|=6,|F1F2|=![]() ,
,
若∠PF2F1为直角,则|PF1|2=|PF2|2+|F1F2|2,可解得:|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,这时
,这时![]() .
.
若∠F2PF1为直角,则|PF1|2+|PF2|2=|F1F2|2,可解得:|PF1|=4,|PF2|=2,这时![]() .
.
解法2:由椭圆的对称性,不妨设P(x,y)(其中x>0,y>0),![]() .若∠PF2F1为直角,则P(
.若∠PF2F1为直角,则P(![]() ),这时|PF1|=
),这时|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,这时
,这时![]() .若∠PF2F1为直角,则由
.若∠PF2F1为直角,则由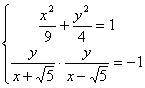 ,解得:
,解得:![]() .
.
于是|PF1|=4,|PF2|=2,这时![]() .
.
点评:由椭圆的方程,熟练准确地写出其几何性质(如顶点,焦点,长、短轴长,焦距,离心率,焦半径等)是应对考试必备的基本功;在解法2中设出了P点坐标的前提下,还可利用|PF1|=a+ex,|PF2|=a-ex来求解.
解析:
由已知,F1不是直角顶点,所以只要对P、F2中哪一个是直角顶点分两种情况即可.

练习册系列答案
相关题目