题目内容
下列命题正确的个数是 ( )
(1)命题“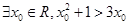 ”的否定是“
”的否定是“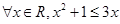 ”;
”;
(2)函数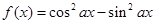 的最小正周期为
的最小正周期为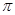 ”是“
”是“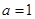 ”的必要不充分条件;
”的必要不充分条件;
(3)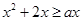 在
在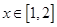 上恒成立
上恒成立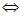
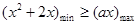 在
在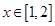 上恒成立
上恒成立
(4) “平面向量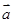 与
与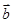 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“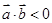 ”。
”。
| A.1 | B.2 | C.3 | D.4 |
B
解析试题分析:命题“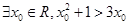 ”的否定是“
”的否定是“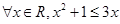 ”为真命题;
”为真命题;
如果函数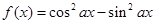 =
= 的最小正周期为
的最小正周期为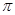 ,那么由
,那么由 得
得 ;
;
由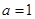 得
得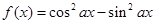 =
= ,其最小正周期为
,其最小正周期为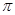 ,所以,(2)是真命题;
,所以,(2)是真命题;
(3)是假命题,正确的方法是由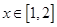 ,可将
,可将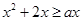 化为
化为 ,所以原命题等价于
,所以原命题等价于 的最小值;
的最小值;
(4)是假命题.因为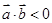 ,有可能
,有可能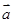 与
与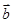 的夹角是
的夹角是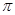 .故选B.
.故选B.
考点:全称命题与存在性命题,充要条件.

练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
“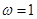 ”是“函数
”是“函数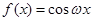 在区间
在区间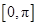 上单调递减”的( )
上单调递减”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
已知 ,
, ,则
,则 是
是 成立的 ( )
成立的 ( )
| A.必要不充分条件 | B.充分不必要条件 |
| C.充要条件 | D.既不充分又不必要条件 |
设条件 ;条件
;条件 ,那么
,那么 是
是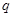 的( ) 条件
的( ) 条件
| A.充分非必要 | B.必要非充分 | C.充分且必要 | D.非充分非必要 |
命题“对任意的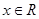 ,都有
,都有 ”的否定为
”的否定为
A.存在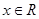 ,使 ,使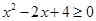 |
B.对任意的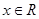 ,都有 ,都有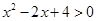 |
C.存在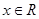 ,使 ,使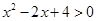 |
D.存在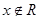 ,使 ,使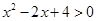 |
设 ,
,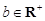 ,则“
,则“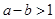 ”是“
”是“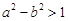 ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
设a,b∈R,则“(a-b)·a2<0”是“a<b”的 ( ).
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
下列命题中,真命题是( ).
| A.?x0∈R,ex0≤0 |
| B.?x∈R,2x>x2 |
C.a+b=0的充要条件是 =-1 =-1 |
| D.a>1,b>1是ab>1的充分条件 |
设a,b为向量,则“|a·b|=|a||b|”是“a∥b”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |