题目内容
命题“对任意的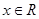 ,都有
,都有 ”的否定为
”的否定为
A.存在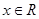 ,使 ,使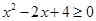 |
B.对任意的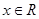 ,都有 ,都有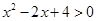 |
C.存在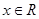 ,使 ,使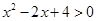 |
D.存在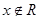 ,使 ,使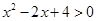 |
C
解析试题分析:全称命题的否定为特称命题,且结论也否定,所以C正确.
考点:逻辑与命题.

练习册系列答案
相关题目
“a=1”是“直线x+y=0和直线x-ay=0互相垂直”的( )
| A.充要条件 | B.必要而不充分条件 |
| C.充分而不必要条件 | D.既不充分也不必要条件 |
下列命题正确的个数是 ( )
(1)命题“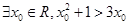 ”的否定是“
”的否定是“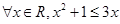 ”;
”;
(2)函数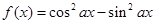 的最小正周期为
的最小正周期为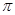 ”是“
”是“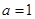 ”的必要不充分条件;
”的必要不充分条件;
(3)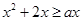 在
在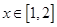 上恒成立
上恒成立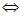
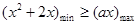 在
在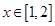 上恒成立
上恒成立
(4) “平面向量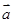 与
与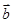 的夹角是钝角”的充分必要条件是“
的夹角是钝角”的充分必要条件是“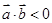 ”。
”。
| A.1 | B.2 | C.3 | D.4 |
下列命题为真命题的是( )
A.若 为真命题,则 为真命题,则 为真命题 为真命题 |
B.“ ”是“ ”是“ ”的充分不必要条件 ”的充分不必要条件 |
C.命题“若 ,则 ,则 ”的否命题为“若 ”的否命题为“若 ,则 ,则 ” ” |
D.若命题 : : ,使 ,使 ,则 ,则 : : ,使 ,使 |
“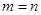 ”是“方程
”是“方程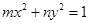 表示圆”的 ( )
表示圆”的 ( )
| A.充分而不必要条件 | B.必要而不充分条件 |
| C.充分必要条件 | D.既不充分也不必要条件 |
“a>1”是“a2>1”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ∈R),则“f(x)是奇函数”是“φ= ”的 ( ).
”的 ( ).
| A.充分不必要条件 | B.充分必要条件 |
| C.必要不充分条件 | D.既不充分也不必要条件 |
 ·
· =
=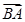 ·
· ,则|
,则| =1;q:y=f(x)是偶函数.
=1;q:y=f(x)是偶函数. B⊆
B⊆