题目内容
设F1、F2是椭圆E: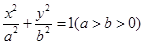 的左、右焦点,P为直线
的左、右焦点,P为直线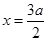 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
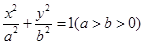 的左、右焦点,P为直线
的左、右焦点,P为直线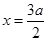 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )A.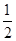 | B. | C. | D. |
C
试题分析:试题分析:根据题意,由于F1、F2是椭圆E:
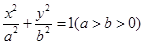 的左、右焦点,P为直线
的左、右焦点,P为直线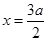 上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"
上一点,那么结合△F2PF1是底角为30°的等腰三角形,F2F1=F2P="2c,"  ,故可知答案为C.
,故可知答案为C.点评:主要是考查了椭圆的几何形性质的运用,属于基础题。

练习册系列答案
相关题目
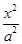 +
+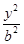 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为 .
. =
= +
+ 成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由. 的焦点在
的焦点在 轴上,离心率
轴上,离心率 ,且经过点
,且经过点 .
.  的直线
的直线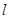 与椭圆
与椭圆 两点,求证:直线
两点,求证:直线 与
与 的倾斜角互补.
的倾斜角互补.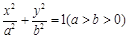 的左焦点为F, 离心率为
的左焦点为F, 离心率为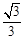 , 过点F且与x轴垂直的直线被椭圆截得的线段长为
, 过点F且与x轴垂直的直线被椭圆截得的线段长为 .
.  , 求k的值.
, 求k的值.  中,若
中,若
 右顶点,则常数
右顶点,则常数 .
.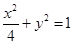 的焦点为
的焦点为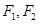 ,点
,点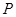 在椭圆上,且线段
在椭圆上,且线段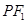 的中点恰好在
的中点恰好在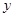 轴上,
轴上,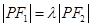 ,则
,则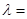 .
.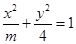 的焦距是2,则
的焦距是2,则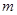 =( )
=( ) 的离心率
的离心率 ,其中一个顶点坐标为
,其中一个顶点坐标为 ,则椭圆的方程为 .
,则椭圆的方程为 .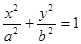 (a>
(a>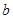 )中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角
)中,记左焦点为F,右顶点为A,短轴上方的端点为B,若角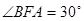 ,则椭圆的离心率为( )
,则椭圆的离心率为( )


