题目内容
【题目】如图，已知圆E：（x+ 
）2+y2=16，点F（ ，0），P是圆E上任意一点．线段PF的垂直平分线和半径PE相交于Q．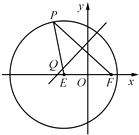 
（1）求动点Q的轨迹Γ的方程；
（2）设直线l与（1）中轨迹Γ相交于A，B两点，直线AO，l，OB的斜率分别为k1 ， k，k2（其中k＞0），若k1 ， k，k2恰好构成公比不为1的等比数列，求k的值．
【答案】
（1）解：连结QF，根据题意，|QP|=|QF|，
则|QE|+|QF|=|QE|+|QP|=4 
，
故动点Q的轨迹Γ是以E，F为焦点，长轴长为4的椭圆．
设其方程为 
，可知a=2， 
，则b=1，
所以点Q的轨迹Γ的方程为 
（2）解：设直线l的方程为：y=kx+m（其中k＞0），A（x1，y1），B（x2，y2），
将直线l的方程代入椭圆方程，消去y整理得：
（1+4k2）x2+8kmx+4m2﹣4=0，
∴x1+x2=﹣ 
，x1x2= 
，且△=16（1+4k2﹣m2）＞0，
∵k1，k，k2恰好构成公比不为1的等比数列，
∴k2=k1k2= 
，
即k2 =k2 +km（﹣ ）+m2，
整理得：m2﹣4k2m2=0，
∵m≠0，
∴k= 
或k=﹣ （舍）
【解析】（1）通过线段PF的垂直平分线和半径PE相交于Q，利用椭圆的定义求动点Q的轨迹Γ的方程；（2）通过设直线l的方程为：y=kx+m（其中k＞0），A（x1 ， y1），B（x2 ， y2），联立直线与椭圆方程、利用韦达定理可知x1+x2=﹣ ，x1x2= ，△=16（1+4k2﹣m2）＞0，利用k2=k1k2代入化简计算即得结论．
练习册系列答案
相关题目
