题目内容
【题目】在三棱柱ABC﹣A1B1C1中,侧面ABB1A1为矩形,AB=1,AA1= ![]() ,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 .
,D为AA1的中点,BD与AB1交于点O,CO⊥侧面ABB1A1 . 
(1)证明:BC⊥AB1;
(2)若OC=OA,求直线C1D与平面ABC所成角的正弦值.
【答案】
(1)证明:由题意,因为ABB1A1是矩形,
D为AA1中点,AB=1,AA1= ![]() ,AD=
,AD= ![]() ,
,
所以在直角三角形ABB1中,tan∠AB1B= ![]() ,
,
在直角三角形ABD中,tan∠ABD= ![]() ,
,
所以∠AB1B=∠ABD,
又∠BAB1+∠AB1B=90°,∠BAB1+∠ABD=90°,
所以在直角三角形ABO中,故∠BOA=90°,
即BD⊥AB1,
又因为CO⊥侧面ABB1A1,AB1侧面ABB1A1,
所以CO⊥AB1
所以,AB1⊥面BCD,
因为BC面BCD,
所以BC⊥AB1.
(2)解:如图,分别以OD,OB1,OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,则A(0,﹣ ![]() ,0),B(﹣
,0),B(﹣ ![]() ,0,0),C(0,0,
,0,0),C(0,0, ![]() ),B1(0,
),B1(0, ![]() ,0),D(
,0),D( ![]() ,0,0),
,0,0),
又因为 ![]() =2
=2 ![]() ,所以
,所以 ![]()
所以 ![]() =(﹣
=(﹣ ![]() ,
, ![]() ,0),
,0), ![]() =(0,
=(0, ![]() ,
, ![]() ),
), ![]() =(
=( ![]() ),
),
设平面ABC的法向量为 ![]() =(x,y,z),
=(x,y,z),
则根据 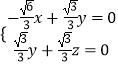 可得
可得 ![]() =(1,
=(1, ![]() ,﹣
,﹣ ![]() )是平面ABC的一个法向量,
)是平面ABC的一个法向量,
设直线C1D与平面ABC所成角为α,则sinα= 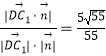 .
.
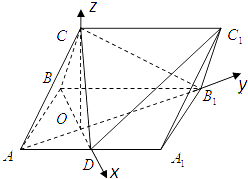
【解析】(1)要证明BC⊥AB1 , 可证明AB1垂直于BC所在的平面BCD,已知CO垂直于侧面ABB1A1 , 所以CO垂直于AB1 , 只要在矩形ABB1A1内证明BD垂直于AB1即可,可利用角的关系加以证明;(2)分别以OD,OB1 , OC所在的直线为x,y,z轴,以O为原点,建立空间直角坐标系,求出 ![]() ,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.
,平面ABC的一个法向量,利用向量的夹角公式,即可得出结论.
【考点精析】掌握空间角的异面直线所成的角和用空间向量求直线与平面的夹角是解答本题的根本,需要知道已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则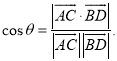 ;设直线
;设直线![]() 的方向向量为
的方向向量为![]() ,平面
,平面![]() 的法向量为
的法向量为![]() ,直线与平面所成的角为
,直线与平面所成的角为![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() , 则
, 则![]() 为
为![]() 的余角或
的余角或![]() 的补角的余角.即有:
的补角的余角.即有: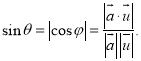 .
.