题目内容
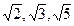 不能为同一等差数列的三项.
不能为同一等差数列的三项. 证明见解析
假设 、
、 、
、 为同一等差数列的三项,则存在整数m,n满足
为同一等差数列的三项,则存在整数m,n满足
 =
= +md ①
+md ①  =
= +nd ②
+nd ②
① n-②
n-② m得:
m得: n-
n- m=
m= (n-m) 两边平方得: 3n2+5m2-2
(n-m) 两边平方得: 3n2+5m2-2 mn=2(n-m)2
mn=2(n-m)2
左边为无理数,右边为有理数,且有理数 无理数
无理数
所以,假设不正确。即 、
、 、
、 不能为同一等差数列的三项
不能为同一等差数列的三项
 、
、 、
、 为同一等差数列的三项,则存在整数m,n满足
为同一等差数列的三项,则存在整数m,n满足 =
= +md ①
+md ①  =
= +nd ②
+nd ②①
 n-②
n-② m得:
m得: n-
n- m=
m= (n-m) 两边平方得: 3n2+5m2-2
(n-m) 两边平方得: 3n2+5m2-2 mn=2(n-m)2
mn=2(n-m)2 左边为无理数,右边为有理数,且有理数
 无理数
无理数所以,假设不正确。即
 、
、 、
、 不能为同一等差数列的三项
不能为同一等差数列的三项
练习册系列答案
相关题目
 试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。
试用反证法证明三条抛物线中至少有一条与x轴的交点不只一个。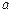 与
与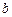 不共面,直线
不共面,直线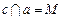 ,直线
,直线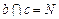 ,又
,又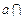 平面
平面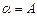 ,
,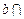 平面
平面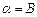 ,
,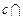 平面
平面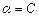 ,求证:
,求证: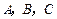 三点不共线.
三点不共线.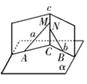
 ,
, ,
, 中至少有一个不小于2”时的假设为_ _____
中至少有一个不小于2”时的假设为_ _____  -
- ≥a+
≥a+ -2.
-2. ,求证
,求证
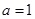 ”是“复数
”是“复数 (
( ,i为虚数单位)是纯虚数”的( )
,i为虚数单位)是纯虚数”的( ) ,…,可归纳出式子( )
,…,可归纳出式子( )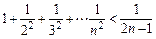



 没有最小数”时,可用反证法证明.
没有最小数”时,可用反证法证明. 是
是 中的最小数,则取
中的最小数,则取 ,可得:
,可得: ,与假设中“
,与假设中“ 是
是 没有最大数”,也可以用反证法证明.我们可以假设
没有最大数”,也可以用反证法证明.我们可以假设 是
是 中的最大数,则可以找到
中的最大数,则可以找到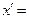 ▲ (用
▲ (用 ,
, 表示),由此可知
表示),由此可知 ,
, ,这与假设矛盾!所以数集
,这与假设矛盾!所以数集