题目内容
设函数f(x)在R上可导，其导函数为f′(x)，且函数y＝(2－x)f′(x)的图像如图所示，则下列结论中一定成立的是( )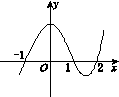
| A．函数f(x)有极大值f(1)和极小值f(－1) |
| B．函数f(x)有极大值f(1)和极小值f(2) |
| C．函数f(x)有极大值f(2)和极小值f(1) |
| D．函数f(x)有极大值f(－1)和极小值f(2) |
A
解析
练习册系列答案
相关题目
曲线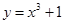
在点
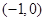处的切线方程为
A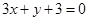． | B． |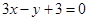
C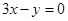． | D． |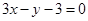
定义在R上的函数
满足
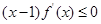，且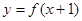
为偶函数，当
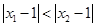时，有（ ）
A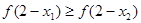． | B． |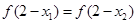
C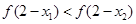． | D． |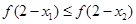
根据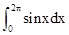
=0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
| A．面积为0 |
| B．曲边梯形在x轴上方的面积大于在x轴下方的面积 |
| C．曲边梯形在x轴上方的面积小于在x轴下方的面积 |
| D．曲边梯形在x轴上方的面积等于在x轴下方的面积 |
定义在R上的函数f(x)满足f(1)＝1且对一切x∈R都有f′(x)<4，则不等式f(x)>4x－3的解集为( )
| A．(－∞，0) | B．(0，＋∞) | C．(－∞，1) | D．(1，＋∞) |
过曲线y＝x3＋x－2上一点P0处的切线平行于直线y＝4x，则点P0的一个坐标是( )
| A．(0，－2) | B．(1，1) | C．(1，4) | D．(－1，－4) |
若S1＝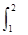
x2dx，S2＝
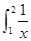dx，S3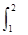＝exdx，则S1，S2，S3的大小关系为( )．
| A．S1<S2<S3 | B．S2<S1<S3 |
| C．S2<S3<S1 | D．S3<S2<S1 |
已知e为自然对数的底数，设函数f(x)＝(ex－1)(x－1)k(k＝1,2)，则( )．
| A．当k＝1时，f(x)在x＝1处取到极小值 |
| B．当k＝1时，f(x)在x＝1处取到极大值 |
| C．当k＝2时，f(x)在x＝1处取到极小值 |
| D．当k＝2时，f(x)在x＝1处取到极大值 |
若点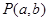
在函数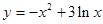
的图像上，点
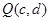在函数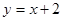
的图像上，则
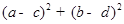的最小值为（ ）
A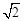． | B．2 | C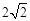． | D．8 |