题目内容
根据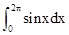 =0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
=0推断直线x=0,x=2π,y=0和正弦曲线y=sinx所围成的曲边梯形的面积时,正确结论为( )
| A.面积为0 |
| B.曲边梯形在x轴上方的面积大于在x轴下方的面积 |
| C.曲边梯形在x轴上方的面积小于在x轴下方的面积 |
| D.曲边梯形在x轴上方的面积等于在x轴下方的面积 |
D
解析

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
函数y=f(x)在定义域(-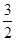 ,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )
,3)内的图像如图所示.记y=f(x)的导函数为y=f¢(x),则不等式f¢(x)≤0的解集为( )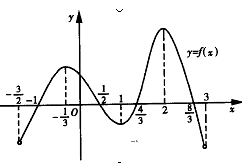
A.[-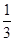 ,1]∪[2,3) ,1]∪[2,3) |
B.[-1,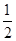 ]∪[ ]∪[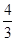 , ,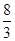 ] ] |
C.[-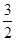 , ,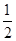 ]∪[1,2) ]∪[1,2) |
D.(-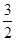 ,- ,-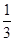 ]∪[ ]∪[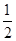 , ,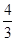 ]∪[ ]∪[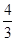 ,3) ,3) |
若实数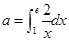 ,则函数
,则函数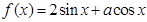 的图象的一条对称轴方程为( )
的图象的一条对称轴方程为( )
A.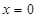 | B. | C.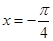 | D.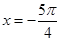 |
若函数 在R上可导,且
在R上可导,且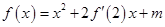 ,则( )
,则( )
A.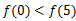 | B.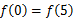 | C.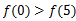 | D.不能确定 |
已知函数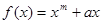 的导数为
的导数为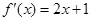 ,则数列
,则数列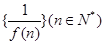 的前
的前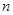 项和是( )
项和是( )
A. | B.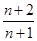 | C.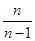 | D.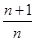 |
已知f(x)=x3+ax2+(a+6)x+1有极大值和极小值,则a的取值范围为( ).
| A.-1<a<2 | B.-3<a<6 |
| C.a<-1或a>2 | D.a<-3或a>6 |
如图,阴影部分的面积是( )
A.2 | B.2- | C. | D. |
函数y=x·e-x在x∈[2,4]上的最小值为( )
| A.0 | B. | C. | D. |
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图像如图所示,则下列结论中一定成立的是( )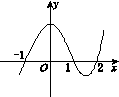
| A.函数f(x)有极大值f(1)和极小值f(-1) |
| B.函数f(x)有极大值f(1)和极小值f(2) |
| C.函数f(x)有极大值f(2)和极小值f(1) |
| D.函数f(x)有极大值f(-1)和极小值f(2) |