题目内容
如图,已知点 ,函数
,函数 的图象上的动点
的图象上的动点 在
在 轴上的射影为
轴上的射影为 ,且点
,且点 在点
在点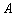 的左侧.设
的左侧.设 ,
, 的面积为
的面积为 .
.
(I)求函数 的解析式及
的解析式及 的取值范围;
的取值范围;
(II)求函数 的最大值.
的最大值.

解:(I)由已知可得 ,所以点
,所以点 的横坐标为
的横坐标为 ,-因为点
,-因为点 在点
在点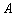 的左侧,所以
的左侧,所以 ,即
,即 .
.
由已知 ,所以
,所以
所以
所以 的面积为
的面积为
(II)
由 ,得
,得 (舍),或
(舍),或 .
.
函数 与
与 在定义域上的情况如下:
在定义域上的情况如下:
|
|
| 2 |
|
|
| + | 0 |
|
|
| ↗ | 极大值 | ↘ |
所以当 时,函数
时,函数 取得最大值8. -
取得最大值8. -

练习册系列答案
相关题目
铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
|
| a | b/万吨 | c/百万元 |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),则购买铁矿石的最少费用为________百万元.



 ,则
,则 的取值范围是( )
的取值范围是( ) B.
B. C.
C. D.
D.
 与双曲线
与双曲线 只有一个公共点,则
只有一个公共点,则 的值有
的值有 个 B.
个 B. 个 C.
个 C. 个 D.无数多个
个 D.无数多个 在
在 上单调递增,则实数
上单调递增,则实数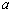 的取值范围( )
的取值范围( )



 在正方形网格中的位置如图所示.设向量
在正方形网格中的位置如图所示.设向量 ,若
,若 ,则实数
,则实数 __________.
__________.
 则2x+3y的最大值为( )
则2x+3y的最大值为( ) ,给出下列三个结论:
,给出下列三个结论: >
> ;②
;②  <
< ; ③
; ③  ,
, 是两条不同的直线,
是两条不同的直线, 是两个不同
是两个不同 的平面,下列命题中正确的是
的平面,下列命题中正确的是 ,
, 
 则
则
 ,则
,则

