题目内容
若a、b∈R*且3a+2b=5，则
+
的最小值为（ ）
| 2 |
| a |
| 3 |
| b |
分析：先把等式3a+2b=5左右两侧同时除以5得1，再把
+
乘以1，再用均值不等式即可得解
| 2 |
| a |
| 3 |
| b |
解答：解：∵3a+2b=5
∴
+
=1
∴
+
=(
+
)×1= (
+
)×(
+
)=
+
+
+
=
+
+
又∵a、b∈R*
∴
＞0 ，
＞0
∴
+
=
+
+
≥
+2
=
当
，即当a=
，b=
时等号成立，取得最小值
故选A
∴
| 3a |
| 5 |
| 2b |
| 5 |
∴
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| 2 |
| a |
| 3 |
| b |
| 3a |
| 5 |
| 2b |
| 5 |
| 6 |
| 5 |
| 4b |
| 5a |
| 9a |
| 5b |
| 6 |
| 5 |
| 12 |
| 5 |
| 4b |
| 5a |
| 9a |
| 5b |
又∵a、b∈R*
∴
| 4b |
| 5a |
| 9a |
| 5b |
∴
| 2 |
| a |
| 3 |
| b |
| 12 |
| 5 |
| 4b |
| 5a |
| 9a |
| 5b |
| 12 |
| 5 |
|
| 24 |
| 5 |
当
|
| 5 |
| 6 |
| 5 |
| 4 |
故选A
点评：本题考查均值不等式以及“1的代换”，要注意均值不等式的条件．属简单题
练习册系列答案
相关题目
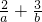的最小值为
的最小值为（ ）