题目内容
(本小题12分)设 ,函数
,函数 的定义域为
的定义域为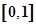 且
且 ,
,
 当
当 时有
时有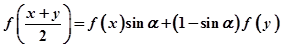
(1)求 ;
;
(2)求 的值;
的值;
(3)求函数 的单调增区间.
的单调增区间.
 ,函数
,函数 的定义域为
的定义域为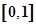 且
且 ,
, 当
当 时有
时有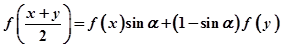
(1)求
 ;
;(2)求
 的值;
的值;(3)求函数
 的单调增区间.
的单调增区间.(1)f(1/2)=sinα,f(1/4)=sin²α; (2)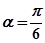
(3) 单调增区间为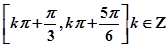 ……12分
……12分
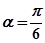
(3) 单调增区间为
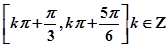 ……12分
……12分(1)由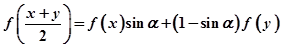 ,根据解题需要给x,y赋予不同的值求解即可.
,根据解题需要给x,y赋予不同的值求解即可.
(3)巧借助第(1)问求得的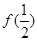 和
和 的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据
的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据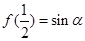 ,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出
,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出 的值.
的值.
(1)对f[(x+y)/2]="f(x)sinα+(1-" sinα)f(y),
令x=1,y=0,得f(1/2)=sinα;……2分
令x=1/2,y=0,得f(1/4)=sin²α;……4分
(2)令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;
令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;
两个f(1/2)相等,得sinα=3sin²α-2 sin³α,结合a∈(0,π/2)可解得sinα=1/2.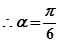 ……8分
……8分
(3)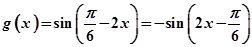
单调增区间为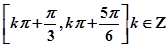 ……12分
……12分
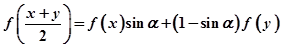 ,根据解题需要给x,y赋予不同的值求解即可.
,根据解题需要给x,y赋予不同的值求解即可.(3)巧借助第(1)问求得的
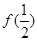 和
和 的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据
的值, 令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;根据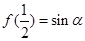 ,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出
,所以sinα=3sin²α-2 sin³α从而解出sinα=1/2,求出 的值.
的值.(1)对f[(x+y)/2]="f(x)sinα+(1-" sinα)f(y),
令x=1,y=0,得f(1/2)=sinα;……2分
令x=1/2,y=0,得f(1/4)=sin²α;……4分
(2)令x=1,y=1/2,得f(3/4)="2" sinα-sin²α;
令x=3/4,y=1/4,得f(1/2)=3sin²α-2 sin³α;
两个f(1/2)相等,得sinα=3sin²α-2 sin³α,结合a∈(0,π/2)可解得sinα=1/2.
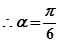 ……8分
……8分(3)
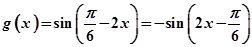
单调增区间为
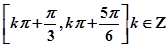 ……12分
……12分
练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 ,设函数
,设函数 +
+
 ,f(x)=
,f(x)= ,求
,求 的值;
的值; ,且满足
,且满足 ,求f(B)的值.
,求f(B)的值.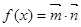 ,其中
,其中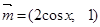 ,
,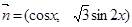
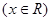 .
.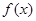 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;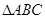 中,
中,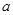 、
、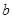 、
、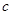 分别是角
分别是角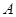 、
、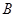 、
、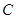 的对边,若
的对边,若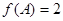 ,
,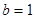 ,
,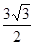 ,求:边
,求:边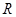 .
. ,函数
,函数 的最大值为
的最大值为 .
. ;
; 的图象向左平移
的图象向左平移 个单位,再将所得图象上各点的横坐标缩短为原来的
个单位,再将所得图象上各点的横坐标缩短为原来的 倍,纵坐标不变,得到函数
倍,纵坐标不变,得到函数 的图象.求
的图象.求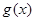 在
在 上的值域.
上的值域.
 的最小正周期;
的最小正周期;
 时,求函数
时,求函数
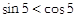
 ,求
,求 时,求函数的值域
时,求函数的值域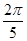 ,半径等于20,则扇形的面积为( )
,半径等于20,则扇形的面积为( )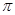
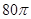
 ,则
,则 ( )
( )


