题目内容
已知数列 的前
的前 项和是
项和是 ,且
,且 .求数列
.求数列 的通项公式;
的通项公式;
【答案】

【解析】
试题分析:由题意根据数列前 项和定义,尽可能对条件
项和定义,尽可能对条件 进行挖掘利用,因为
进行挖掘利用,因为 ,所以由条件可求出数列
,所以由条件可求出数列 的首项
的首项 ,当
,当 时,有
时,有 ,由条件可得
,由条件可得 ,即
,即 ,从而发现数列
,从而发现数列 是以首项为
是以首项为 ,公比为
,公比为 的等比数列,再由等比数列的通项公式可求得数列
的等比数列,再由等比数列的通项公式可求得数列 的通项公式.
的通项公式.
试题解析:当 时,
时, ,
, ,∴
,∴ ; 2分
; 2分
当 时,
时, 4分
4分
两式相减得 ,即
,即 ,又
,又 ,∴
,∴ 8分
8分
∴数列 是以
是以 为首项,
为首项, 为公比的等比数列. 10分
为公比的等比数列. 10分
∴ 12分
12分
考点:1.数列前 项和定义;2.等比数列.
项和定义;2.等比数列.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的前
的前 项和是
项和是 ,且
,且 .
. ,求数列
,求数列 的前
的前 .
. 的前
的前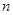 项和是
项和是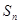 ,满足
,满足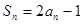 .
. 及前
及前 满足
满足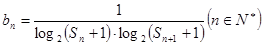 ,求数列
,求数列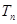 ;
;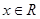 ,恒有
,恒有 成立,求实数
成立,求实数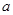 的取值范围
的取值范围 的前
的前 项和是
项和是 ,满足
,满足 .
. 及前
及前 满足
满足 ,求数列
,求数列 ;
; ,恒有
,恒有 成立,求实数
成立,求实数 的取值范围.
的取值范围. 的前
的前 项和是
项和是 ,且
,且 .
. ,求数列
,求数列 的前
的前
 的前
的前 项和
项和 是实数),下列结论正确的是 (
)
是实数),下列结论正确的是 (
) 为任意实数,
为任意实数, 均是等比数列
均是等比数列  时,
时, 时,
时, 时,
时,