题目内容
已知函数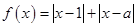 .
.
(1)当 时,解不等式
时,解不等式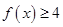 ;
;
(2)若不等式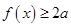 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(1) ;(2)
;(2) .
.
解析试题分析:(1)将 代入函数
代入函数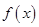 的解析式,利用零点分段法将区间分成三段,去绝对值符号,并求出相应的不等式;(2)将问题转化为
的解析式,利用零点分段法将区间分成三段,去绝对值符号,并求出相应的不等式;(2)将问题转化为 ,利用双绝对值函数
,利用双绝对值函数 的最小值为
的最小值为
 ,于是得到
,于是得到 ,问题转化为
,问题转化为 来求解,解出不等式
来求解,解出不等式 即可.
即可.
(1)由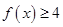 得,
得, ,或
,或 ,或
,或 ,
,
解得: 或
或 ,原不等式的解集为
,原不等式的解集为 ;
;
(2)由不等式的性质得: ,
,
要使不等式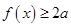 恒成立,则
恒成立,则 ,
,
解得: 或
或
所以实数 的取值范围为
的取值范围为 .
.
考点:1.零点分段法求解不等式;2.不等式恒成立

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
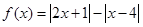
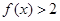 ;
; 的最小值.
的最小值.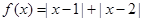
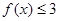 的解集;
的解集;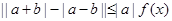 (
(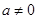 ,
,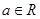 ,
,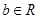 )恒成立,求实数
)恒成立,求实数 的范围.
的范围.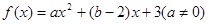 .
.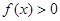 的解集为
的解集为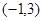 .求
.求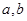 的值;
的值;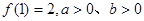 求
求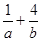 的最小值.
的最小值.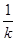 },求k的值;
},求k的值;
 的解集.
的解集. 的不等式
的不等式 存在实数解,则实数
存在实数解,则实数 的取值范围是 。
的取值范围是 。