题目内容
(本小题满分13分)已知椭圆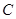 :
: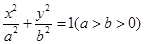 的右焦点为
的右焦点为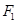
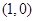 ,离心率为
,离心率为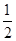 .
.
(Ⅰ)求椭圆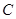 的方程及左顶点
的方程及左顶点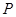 的坐标;
的坐标;
(Ⅱ)设过点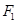 的直线交椭圆
的直线交椭圆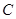 于
于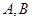 两点,若
两点,若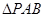 的面积为
的面积为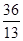 ,求直线
,求直线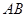 的方程.
的方程.
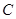 :
: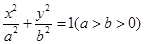 的右焦点为
的右焦点为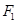
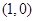 ,离心率为
,离心率为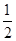 .
.(Ⅰ)求椭圆
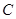 的方程及左顶点
的方程及左顶点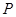 的坐标;
的坐标;(Ⅱ)设过点
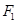 的直线交椭圆
的直线交椭圆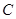 于
于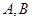 两点,若
两点,若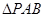 的面积为
的面积为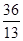 ,求直线
,求直线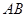 的方程.
的方程.(19)(本小题满分13分)
解:(Ⅰ)由题意可知: ,
, ,所以
,所以 .
.
所以 .
.
所以椭圆 的标准方程为
的标准方程为 ,左顶点
,左顶点 的坐标是
的坐标是 .
.
………………………………4分
(Ⅱ)根据题意可设直线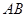 的方程为
的方程为 ,
, .
.
由 可得:
可得: .
.
所以 ,
, ,
, .
.
……………………………………7分
所以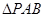 的面积
的面积
……………………………………9分
 .
.
………………………………………10分
因为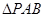 的面积为
的面积为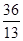 ,
,
所以 .
.
令 ,则
,则 .
.
解得 (舍),
(舍), .
.
所以 .
.
所以直线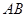 的方程为
的方程为 或
或 .
.
……………………………………13分
解:(Ⅰ)由题意可知:
 ,
, ,所以
,所以 .
. 所以
 .
. 所以椭圆
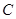 的标准方程为
的标准方程为 ,左顶点
,左顶点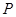 的坐标是
的坐标是 .
. ………………………………4分
(Ⅱ)根据题意可设直线
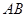 的方程为
的方程为 ,
, .
.由
 可得:
可得: .
.所以
 ,
, ,
, .
. ……………………………………7分
所以
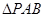 的面积
的面积
……………………………………9分
 .
.………………………………………10分
因为
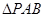 的面积为
的面积为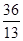 ,
,所以
 .
.令
 ,则
,则 .
.解得
 (舍),
(舍), .
.所以
 .
. 所以直线
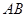 的方程为
的方程为 或
或 .
.……………………………………13分
略

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
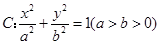 的中心在原点,它的左右两个焦点分别为
的中心在原点,它的左右两个焦点分别为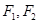 ,过右焦点
,过右焦点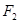 且与
且与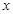 轴垂直的直线
轴垂直的直线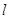 与椭圆
与椭圆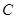 相交,其中一个交点为
相交,其中一个交点为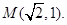
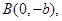 直线
直线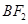 交椭圆
交椭圆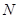 ,求
,求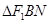 的面积.
的面积.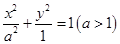 的左、右焦点分别为
的左、右焦点分别为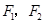
 ,
,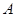 是椭圆上位于
是椭圆上位于 轴上方的动点 (Ⅰ)当
轴上方的动点 (Ⅰ)当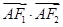 取最小值时,求
取最小值时,求 的离心率为
的离心率为 ,右焦点到直线
,右焦点到直线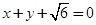 的距离为
的距离为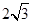 ,过
,过 的直线
的直线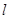 交椭圆于
交椭圆于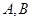 两点
两点 .
.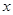 轴于
轴于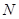 ,
,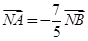 ,求直线
,求直线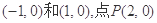 在椭圆上,则椭圆的方程为( )
在椭圆上,则椭圆的方程为( )



 ,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若
,过椭圆的右焦点且与x轴垂直的直线与椭圆交于P、Q两点,椭圆的右准线与x轴交于点M,若 为正三角形,则椭圆的离心率等于 ▲
为正三角形,则椭圆的离心率等于 ▲  ,它的两个焦点为F1、F2,若| F1F2|=8, 弦AB过F1 ,则△ABF2的周长为 ▲
,它的两个焦点为F1、F2,若| F1F2|=8, 弦AB过F1 ,则△ABF2的周长为 ▲  的左,右两个焦点分别为
的左,右两个焦点分别为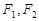 ,短轴的上端点为
,短轴的上端点为 ,短轴上的两个三等分点为
,短轴上的两个三等分点为 ,且
,且 为正方形,若过点
为正方形,若过点 轴上的一个截距为
轴上的一个截距为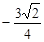 ,则此椭圆方程的方程为 ▲ .
,则此椭圆方程的方程为 ▲ .