题目内容
已知函数 .
.
(1)已知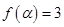 ,且
,且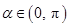 ,求
,求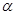 的值;
的值;
(2) 求函数
求函数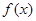 的单调递增区间;
的单调递增区间;
(3)若对任意的x∈ ,不等式
,不等式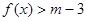 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
(1)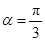 .(2)函数
.(2)函数 的单调增区间为
的单调增区间为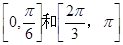 .(3) m<4 。
.(3) m<4 。
解析试题分析:(1)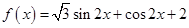 =
=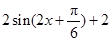 .
.
由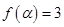 ,得
,得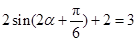 .
.
∴ .
.
∴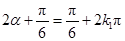 ,或
,或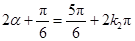
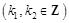 ,
,
即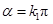 或
或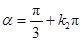
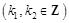 .
. 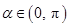 ,∴
,∴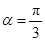 .
.
(2)由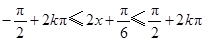 ,得
,得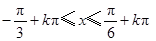 .
.
∴函数 的单调增区间为
的单调增区间为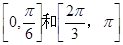 .
.
(3) 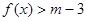 恒成立,即
恒成立,即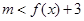 恒成立,所以只需
恒成立,所以只需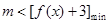 ,而x∈
,而x∈ 时,
时,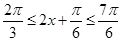 ,
, 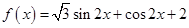 =
=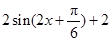 最小值为1,所以
最小值为1,所以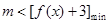 =4,即m<4 。
=4,即m<4 。
考点:本题主要考查三角函数和差倍半公式的应用,三角函数的性质,不等式恒成立问题。
点评:典型题,三角函数的图象和性质、三角函数图象的变换是高考考查的重点,为研究三角函数的性质,往往要利用诱导公式、和差倍半公式进行“化一” 。(II)研究三角函数单调区间,遵循“内外层函数,同增异减”。(3)不等式的恒成立问题,往往通过“分离参数”转化成求函数最值。

练习册系列答案
相关题目
 和
和 ,若它们的最小正周期的和为
,若它们的最小正周期的和为 ,且
,且 ,
, ,
, 和
和 的解析式。
的解析式。 .
. ,求
,求 的最大值及此时相应的
的最大值及此时相应的 的值;
的值; 、b、c分别为角A、B、C的对边,若
、b、c分别为角A、B、C的对边,若 ,b =l,
,b =l, ,求
,求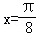 .
.
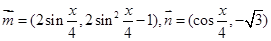 ,函数
,函数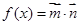 .
.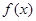 的最大值,并写出相应
的最大值,并写出相应 的取值集合;
的取值集合;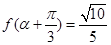 ,且
,且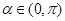 ,求
,求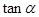 的值.
的值.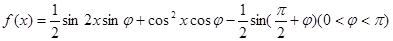 ,其图象过点
,其图象过点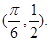
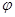 的值;
的值; 的图象上各点的横坐标缩短到原来的
的图象上各点的横坐标缩短到原来的 ,纵坐标不变,得到函数
,纵坐标不变,得到函数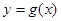 的图象,求函数
的图象,求函数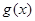 在
在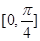 上的最大值和最小值。
上的最大值和最小值。 .
.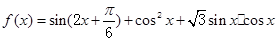 .
.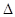 ABC的三个内角,若cosB=
ABC的三个内角,若cosB=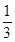 ,
,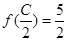 ,求sinA.
,求sinA.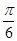 )+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为
)+1(A>0,ω>0)的最大值为3,其图象相邻两条对称轴之间的距离为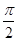 .
. )=2,求α的值.
)=2,求α的值.