题目内容
20.长度为5的线段AB的两端点A,B分别在x轴、y轴上滑动,点M在线段AB上,且AM=2,则点M的轨迹方程是$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1.分析 先设M(x,y),A(a,0),B(0,b),根据$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{MB}$得x,y的方程,最后根据a2+b2=25得出x,y的关系即M的轨迹方程.
解答 解:设M(x,y),A(a,0),B(0,b),
由$\overrightarrow{AM}=\frac{2}{3}\overrightarrow{MB}$得(x-a,y)=$\frac{2}{3}$(-x,b-y),
∴$\left\{\begin{array}{l}{x-a=-\frac{2}{3}x}\\{y=\frac{2}{3}(b-y)}\end{array}\right.$,解得x=$\frac{3}{5}a$,y=$\frac{2}{5}$b
∵|AB|=5
∴a2+b2=25
∴$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1.
故答案为$\frac{{x}^{2}}{9}+\frac{{y}^{2}}{4}$=1.
点评 本题主要考查了椭圆的标准方程.本题主要灵活利用了向量的关系进行解题.

练习册系列答案
相关题目
10.直线kx-y+1=3k中,无论k如何变动,直线都恒过定点( )
| A. | (0,0) | B. | (0,1) | C. | (3,1) | D. | (2,1) |
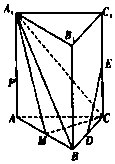 如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.
如图,正三棱柱ABC-A1B1C1中,D,E,M分别是线段BC,CC1,AB的中点,AA1=2AB=4.