题目内容
(本小题满分12分)
已知数列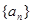 是等比数列,
是等比数列,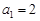 ,且
,且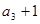 是
是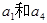 的等差中项.
的等差中项.
(Ⅰ) 求数列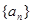 的通项公式
的通项公式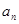 ;
;
(Ⅱ)若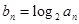 ,求数列
,求数列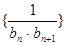 的前n项和
的前n项和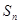 .
.
(1)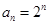 ;(2)
;(2)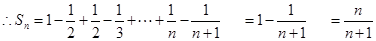 。
。
解析试题分析:
(1)设数列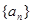 的公比为q
的公比为q (1分)
(1分)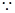
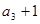 是
是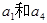 的等差中项
的等差中项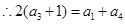 解得q ="2"
解得q ="2"
又因为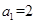 所以
所以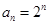 (6分)
(6分)
(2)
 (12分)
(12分)
考点:本题主要考查等差数列、等比数列的的基础知识,“裂项相消法”。
点评:中档题,本题综合考查等差数列、等比数列的基础知识,本解答从确定函数通项公式入手,明确了所研究数列的特征。“错位相消法”是高考常常考到数列求和方法。

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
已知函数f(n)= ,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
,且an=f(n)+f(n+1),则a1+a2+a3+…+a2014等于( )
| A.-2013 | B.-2014 | C.2013 | D.2014 |
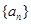 的前
的前 项和为
项和为 ,
, ,且
,且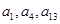 成等比数列.
成等比数列.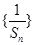 的前
的前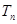 的表达式。
的表达式。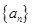 的前
的前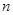 项和
项和 。
。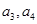 ;
;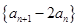 是等比数列;
是等比数列; 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和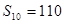 且
且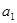 ,
,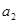 ,
,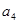 成等比数列.(Ⅰ)证明
成等比数列.(Ⅰ)证明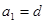 ; (Ⅱ)求公差
; (Ⅱ)求公差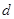 的值和数列
的值和数列 满足
满足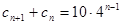 ,
, ,数列
,数列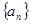 满足
满足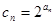
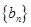 满足
满足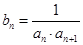 ,
,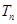 为数列
为数列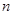 项和.求
项和.求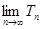 ;(5分)
;(5分)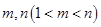 ,使得
,使得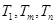 成等比数列?若存在,求出所有
成等比数列?若存在,求出所有 的值;若不存在,请说明理由.(6分)
的值;若不存在,请说明理由.(6分) 前n项和
前n项和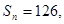 求
求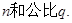
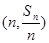 在直线
在直线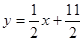 上.数列{bn}满足
上.数列{bn}满足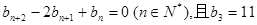 ,前9项和为153.
,前9项和为153.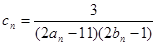 ,数列{cn}的前n和为Tn,求使不等式
,数列{cn}的前n和为Tn,求使不等式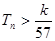 对一切
对一切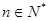 都成立的最大正整数k的值.
都成立的最大正整数k的值.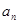 }的前
}的前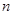 项和为
项和为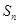 ,已知对任意的
,已知对任意的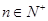 ,点
,点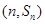 均在函数
均在函数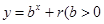 且
且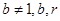 均为常数)的图像上.
均为常数)的图像上.  的值;
的值; 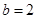 时,记
时,记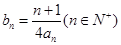 ,求数列
,求数列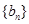 的前
的前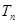 .
.