题目内容
设数列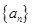
的前
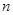项和
。
（1）求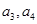
；
（2）证明：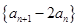
是等比数列；
（1）
（2）先构造
，作差得到递推式化简从而证明.
解析试题分析：（1）
（2）由题设
所以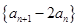是首项为2，公比为2的等比数列
考点：等比数列 数列的和
点评：本题的关键是利用当
时，
间的关系，消掉
从而得到递推公式.
练习册系列答案
开心蛙口算题卡系列答案
相关题目
开心蛙口算题卡系列答案题目内容
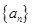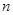设数列的前项和。
（1）求；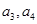
（2）证明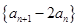：是等比数列；
（1）（2）先构造，作差得到递推式化简从而证明.
解析试题分析：（1）
（2）由题设
所以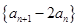是首项为2，公比为2的等比数列
考点：等比数列 数列的和
点评：本题的关键是利用当时，间的关系，消掉从而得到递推公式.
开心蛙口算题卡系列答案
中，
求数列{
}的前
项和
满足：
，其中
为数列
项和.
满足：
，试求
.
满足
，
是
，
的等差中项。
，求数列
的前
项和
。
中，
为常数，
，且
成公比不等于1的等比数列.
的值；
，求数列
的前
项和
。
满足
，且
是
，
的等差中项.
，
，求使 
成立的正整数
的最小值.
前
项和为
，首项为
，且
等差数列.
，设
，求数列
的前
.
是等比数列，
，且
是
的等差中项.
；
，求数列
的前n项和
.
和
满足：
，
，
，
（2）数列
是等差数列，并求出其公差；
，
和
的值．