题目内容
(本小题12分)设 是一个公差为
是一个公差为 的等差数列,它的前10项和
的等差数列,它的前10项和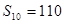 且
且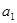 ,
,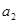 ,
,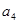 成等比数列.(Ⅰ)证明
成等比数列.(Ⅰ)证明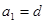 ; (Ⅱ)求公差
; (Ⅱ)求公差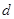 的值和数列
的值和数列 的通项公式。
的通项公式。
(1)根据已知中的 成等比数列,结合等差数列的通项公式得到
成等比数列,结合等差数列的通项公式得到
(2)
解析试题分析:(Ⅰ)证明:∵ 成等比数列,∴
成等比数列,∴ .
.
而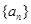 是等差数列,有
是等差数列,有 ,于是
,于是
即 ,化简得
,化简得 .
.
(Ⅱ)解:由条件 和
和 得到
得到
由(Ⅰ)知 代入上式得
代入上式得 故
故
考点:等差数列
点评:解决该试题的关键是对于等比数列和等差数列的通项公式的准确运用。属于基础题。

练习册系列答案
相关题目
已知函数f(x)=xa的图象过点(4,2),令an=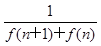 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
A.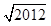 -1 -1 | B. -1 -1 | C.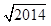 -1 -1 | D.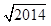 +1 +1 |
 前
前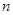 项和
项和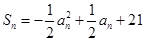 ,且
,且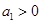 ;
;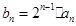 ,求
,求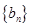 前
前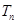 .
.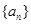 满足
满足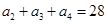 ,
,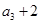 是
是 ,
,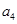 的等差中项。
的等差中项。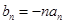 ,求数列
,求数列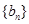 的前
的前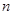 项和
项和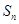 。
。 满足
满足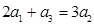 ,且
,且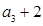 是
是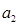 ,
,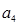 的等差中项.
的等差中项. ,
,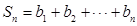 ,求使
,求使  成立的正整数
成立的正整数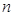 的最小值.
的最小值.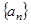 前
前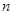 项和为
项和为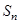 ,首项为
,首项为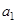 ,且
,且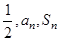 等差数列.
等差数列.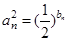 ,设
,设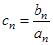 ,求数列
,求数列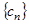 的前
的前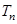 .
. 的相邻两项
的相邻两项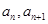 是关于
是关于 的方程
的方程 的两根,且
的两根,且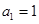
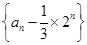 是等比数列;
是等比数列; 项和
项和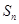 ;
;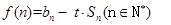 若
若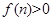 对任意的
对任意的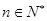 都成立,求
都成立,求 的取值范围。
的取值范围。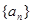 是等比数列,
是等比数列,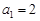 ,且
,且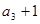 是
是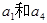 的等差中项.
的等差中项.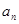 ;
;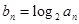 ,求数列
,求数列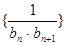 的前n项和
的前n项和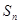 .
.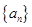 的各项均为正数,且
的各项均为正数,且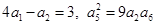 . (1)求数列
. (1)求数列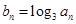 ,求数列
,求数列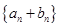 的前
的前 项和
项和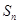 .
.