题目内容
(本小题满分12分)
等比数列{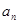 }的前
}的前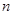 项和为
项和为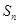 ,已知对任意的
,已知对任意的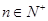 ,点
,点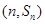 均在函数
均在函数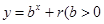 且
且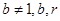 均为常数)的图像上.
均为常数)的图像上.
(1)求 的值;
的值;
(2)当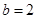 时,记
时,记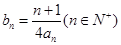 ,求数列
,求数列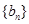 的前
的前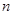 项和
项和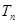 .
.
(1) (2)
(2)
解析试题分析:(1)因为对任意的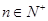 ,点
,点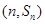 均在函数
均在函数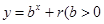 且
且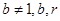 均为常数)的图像上.所以得
均为常数)的图像上.所以得 . ……2分
. ……2分
当 时,
时, ,
,
当 时,
时, , ……4分
, ……4分
又因为{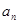 }为等比数列,所以
}为等比数列,所以 ,公比为
,公比为 ,所以
,所以 . ……6分
. ……6分
(2)当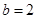 时,
时, ,
, ,
,
则

两式相减,得
=

所以 ……12分
……12分
考点:本题主要考查了等比数列的定义,通项公式,以及已知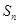 求
求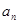 的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前
的基本题型,并运用错位相减法求出一等比数列与一等差数列对应项乘积所得新数列的前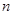 项和
项和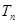 .
.
点评:由前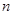 项和
项和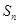 求
求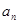 时,不要忘记分
时,不要忘记分 和
和 两种情况讨论;错位相减法求前
两种情况讨论;错位相减法求前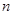 项和
项和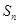 是高考中常考的内容,求解过程中一般运算比较麻烦,学生容易出现错误,所以求解时一定要细心.
是高考中常考的内容,求解过程中一般运算比较麻烦,学生容易出现错误,所以求解时一定要细心.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
已知函数f(x)=xa的图象过点(4,2),令an=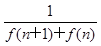 ,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
,n∈N*.记数列{an}的前n项和为Sn,则S2 013=( )
A.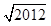 -1 -1 | B. -1 -1 | C.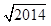 -1 -1 | D.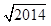 +1 +1 |
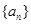 满足
满足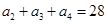 ,
,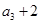 是
是 ,
,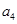 的等差中项。
的等差中项。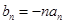 ,求数列
,求数列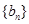 的前
的前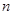 项和
项和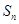 。
。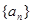 是等比数列,
是等比数列,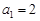 ,且
,且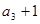 是
是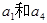 的等差中项.
的等差中项.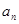 ;
;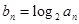 ,求数列
,求数列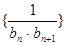 的前n项和
的前n项和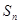 .
.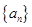 的各项均为正数,且
的各项均为正数,且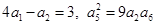 . (1)求数列
. (1)求数列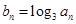 ,求数列
,求数列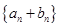 的前
的前 项和
项和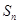 .
.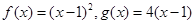 ,数列
,数列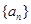 满足
满足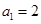 ,且
,且 .
.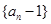 是否是等比数列?(5分)
是否是等比数列?(5分)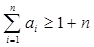 .(5分)
.(5分) 和
和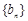 满足:
满足: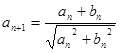 ,
,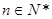 ,
,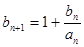 ,
,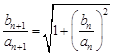 (2)数列
(2)数列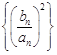 是等差数列,并求出其公差;
是等差数列,并求出其公差;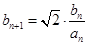 ,
,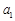 和
和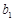 的值.
的值.
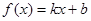 的图像经过点
的图像经过点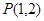 和
和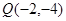 ,令
,令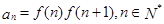 ,记数列
,记数列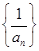 的前项和为
的前项和为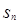 ,当
,当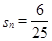 时,
时, 的值等于( )
的值等于( )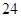
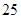
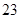
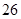
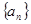 中,
中,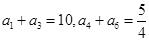 ,求
,求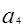 及其前5项的和
及其前5项的和 .
.