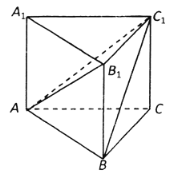
题目内容
【题目】如图,在三棱柱![]() 中,已知
中,已知![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 的中点,
的中点,![]() 与
与![]() 所成角的大小为90°,且
所成角的大小为90°,且![]() .
.
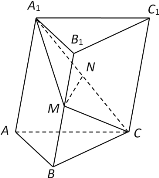
求证:(1)平面![]() 平面
平面![]() ;
;
(2)![]() 平面
平面![]() .
.
【答案】(1)见解析;(2)见解析
【解析】
(1)推导出![]() ,
,![]() ,从而
,从而![]() 平面
平面![]() ,由此能证明平面
,由此能证明平面![]() 平面
平面![]() .
.
(2)取![]() 中点
中点![]() ,连结
,连结![]() ,
,![]() ,推导出四边形
,推导出四边形![]() 是平行四边形,从而
是平行四边形,从而![]() ,由此能证明
,由此能证明![]() 平面
平面![]() .
.
证明:(1)因为![]() 与
与![]() 所成角的大小为90°,所以
所成角的大小为90°,所以![]() ⊥
⊥![]() ,
,
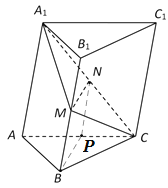
因为![]() ,且N是A1C的中点,所以
,且N是A1C的中点,所以![]() ⊥
⊥![]() .
.
又![]() ,
,![]() 、
、![]() 平面
平面![]() ,
,
故![]() ⊥平面
⊥平面![]() ,
,
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() ⊥平面
⊥平面![]() .
.
(2)取AC中点P,连结NP,BP.
因为N为A1C中点,P为AC中点,所以PN//AA1,且PN![]() AA1.
AA1.
在三棱柱![]() 中,BB1 // AA1,且BB1
中,BB1 // AA1,且BB1![]() AA1.
AA1.
又M为BB1中点,故BM // AA1,且BM![]() AA1.
AA1.
所以PN // BM,且PN![]() BM,于是四边形PNMB是平行四边形,
BM,于是四边形PNMB是平行四边形,
从而MN // BP.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
故![]() 平面
平面![]() .
.

练习册系列答案
相关题目
【题目】某人某天的工作是驾车从![]() 地出发,到
地出发,到![]() 两地办事,最后返回
两地办事,最后返回![]() 地,
地,![]() ,三地之间各路段行驶时间及拥堵概率如下表
,三地之间各路段行驶时间及拥堵概率如下表
路段 | 正常行驶所用时间(小时) | 上午拥堵概率 | 下午拥堵概率 |
| 1 | 0.3 | 0.6 |
| 2 | 0.2 | 0.7 |
| 3 | 0.3 | 0.9 |
若在某路段遇到拥堵,则在该路段行驶时间需要延长1小时.
现有如下两个方案:
方案甲:上午从![]() 地出发到
地出发到![]() 地办事然后到达
地办事然后到达![]() 地,下午从
地,下午从![]() 地办事后返回
地办事后返回![]() 地;
地;
方案乙:上午从![]() 地出发到
地出发到![]() 地办事,下午从
地办事,下午从![]() 地出发到达
地出发到达![]() 地,办完事后返回
地,办完事后返回![]() 地.
地.
(1)若此人早上8点从![]() 地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回
地出发,在各地办事及午餐的累积时间为2小时,且采用方案甲,求他当日18点或18点之前能返回![]() 地的概率.
地的概率.
(2)甲乙两个方案中,哪个方案有利于办完事后更早返回![]() 地?请说明理由.
地?请说明理由.