题目内容
1.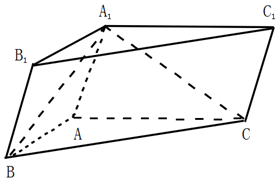 如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形.
如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形.(1)求证△A1BC为等腰三角形;
(2)若$∠{A_1}BC=\frac{π}{3}$,AB⊥AC,平面A1BC⊥平面ABC,求二面角B-A1C-C1的余弦值.
分析 (1)取BC中点D,连接A1D,AD,则AD⊥BC,证明BC⊥平面A1AD,可得BC⊥A1D,即可证明△A1BC为等腰三角形;
(2)建立如图所示的坐标系,利用向量方法求二面角B-A1C-C1的余弦值.
解答 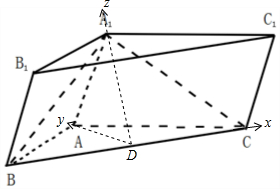 (1)证明:取BC中点D,连接A1D,AD,则AD⊥BC,
(1)证明:取BC中点D,连接A1D,AD,则AD⊥BC,
∵四边形BCC1B1为矩形,∴BC⊥A1A,
∵AD∩A1A=A,∴BC⊥平面A1AD,
∴BC⊥A1D,
∵BD=DC,
∴△A1BC为等腰三角形;
(2)解:由题意,A1D⊥平面ABC,则建立如图所示的坐标系,设AB=2,则C($\sqrt{2}$,0,0),A(0,$\sqrt{2}$,0),A1(0,0,$\sqrt{6}$),∴$\overrightarrow{AC}$=($\sqrt{2}$,-$\sqrt{2}$,0),$\overrightarrow{A{A}_{1}}$=(0,-$\sqrt{2}$,$\sqrt{6}$),
设平面A1C的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\sqrt{2}x-\sqrt{2}y=0}\\{-\sqrt{2}y+\sqrt{6}z=0}\end{array}\right.$,取$\overrightarrow{n}$=($\sqrt{3}$,$\sqrt{3}$,1),
∵平面A1BC的一个法向量为(0,1,0),则二面角B-A1C-C1的余弦值=$\frac{\sqrt{3}}{\sqrt{3+3+1}•1}$=$\frac{\sqrt{21}}{7}$.
点评 本题考查线面垂直的证明,考查二面角余弦值的计算,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
3.已知集合A={x|x2-x-2<0},B={y|y=ex,x<ln3},则A∪B=( )
| A. | (-1,3) | B. | (-1,0) | C. | (0,2) | D. | (2,3) |
10. 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
 如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )
如图,在矩形ABCD中,AB=4,BC=6,四边形AEFG为边长为2的正方形,现将矩形ABCD沿过点的动直线l翻折的点C在平面AEFG上的射影C1落在直线AB上,若点C在抓痕l上的射影为C2,则$\frac{{C}_{1}{C}_{2}}{C{C}_{2}}$的最小值为( )| A. | 6$\sqrt{5}$-13 | B. | $\sqrt{5}$-2 | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
 ,则
,则 等于( )
等于( ) B.
B. C.
C. D.
D.
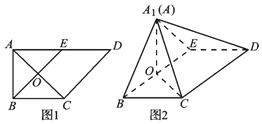 如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE.
如图1,在直角梯形ABCD中,AD∥BC,∠BAD=$\frac{π}{2}$,AB=BC=1,AD=2,E是AD的中点,O是AC与BE的交点.将△ABE沿BE折起到图22中△A1BE的位置,得到四棱锥A1-BCDE. 如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.
如图,三棱锥P-ABC中,PB⊥底面ABC,∠BCA=90°,PB=BC=CA=2,E为PC的中点,点F在PA上,且2PF=FA.