题目内容
6.已知抛物线C:y2=2px(p>0)以x=-2为准线方程,过x轴上一定点P(3,0)作直线l与抛物线交于不同的两点A、B(1)求抛物线C的标准方程;
(2)求弦AB的中点M的轨迹方程.
分析 (1)抛物线C:y2=2px(p>0)以x=-2为准线方程,可得p=4,然后求解抛物线C的标准方程.
(2)设A(x1,y1),B(x2,y2),M(x,y),利用平方差法求解轨迹方程即可.
解答 (本小题满分12分)
解:(1)抛物线C:y2=2px(p>0)以x=-2为准线方程,
可得p=4,抛物线C的标准方程y2=8x----(4分)
(2)设A(x1,y1),B(x2,y2),M(x,y),
$\left\{\begin{array}{l}{{{y}_{1}}^{2}=8{x}_{1}}\\{{{y}_{2}}^{2}=8{x}_{2}}\end{array}\right.$ 两式作差得(y1-y2)(y1+y2)=8(x1-x2),
当x1≠x2时,有$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{8}{{y}_{1}+{y}_{2}}$,${k}_{AB}=\frac{8}{2y}$=$\frac{y-0}{x-3}$,
∴y2=4x-12----(8分)
当x1=x2时,即弦AB⊥x轴,又∵AB中的P(3,0),∴x1=x2=3,
此时弦AB的中点M的坐标为(3,0),经验证满足y2=4x-12
综上所述,弦AB的中点M的轨迹方程为y2=4x-12----(12分)
点评 本题考查抛物线的简单性质,标准方程的求法,曲线的轨迹方程的求法,平方差法的应用,考查计算能力.

练习册系列答案
 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
8.下列命题,其中说法错误的是( )
| A. | 双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{3}$=1的焦点到其渐近线距离为$\sqrt{3}$ | |
| B. | 若命题p:?x∈R,使得sinx+cosx≥2,则¬p:?x∈R,都有sinx+cosx<2 | |
| C. | 若p∧q是假命题,则p、q都是假命题 | |
| D. | 设a,b是互不垂直的两条异面直线,则存在唯一平面α,使得a?α,且b∥α |
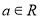 ,则“
,则“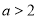 ”是“
”是“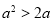 ”的( )
”的( ) 如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.
如图,四棱锥P-ABCD的底面为梯形,且AB∥DC,DC=2AB,E和F分别是棱CD和PC的中点,PD⊥CD,PB=BC=BD=2$\sqrt{3}$,AB=2,二面角P-AB-D为$\frac{2π}{3}$.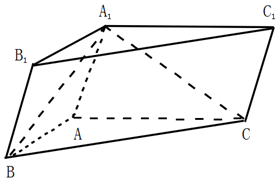 如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形.
如图所示,在三棱柱ABC-A1B1C1中,AB=AC,四边形BCC1B1为矩形. 如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.PO=$\sqrt{2}$,AB=2.求证:
如图,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,E是PC的中点.PO=$\sqrt{2}$,AB=2.求证: 在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.
在四棱锥P-ABCD中,△ABC,△ACD都为等腰直角三角形,∠ABC=∠ACD=90°,△PAC是边长为2的等边三角形,PB=$\sqrt{2}$,E为PA的中点.