Question

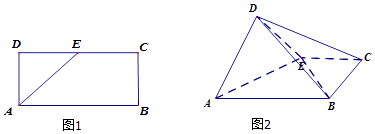
【题目】已知四棱锥P﹣ABCD的正视图1是一个底边长为4、腰长为3的等腰三角形，图2、图53分别是四棱锥P﹣ABCD的侧视图和俯视图．
（1）求证：AD⊥PC；
（2）求四棱锥P﹣ABCD的侧面积．

Answer 1

【答案】
（1）证明：依题意，可知点P在平面ABCD上的正射影是线段CD的中点E，连接PE，

则PE⊥平面ABCD．

∵AD平面ABCD，

∴AD⊥PE．

∵AD⊥CD，CD∩PE=E，CD平面PCD，PE平面PCD，

∴AD⊥平面PCD．

∵PC平面PCD，

∴AD⊥PC．

（2）解：依题意，在等腰三角形PCD中，PC=PD=3，DE=EC=2，

在Rt△PED中， ，

过E作EF⊥AB，垂足为F，连接PF，

∵PE⊥平面ABCD，AB平面ABCD，

∴AB⊥PE．

∵EF平面PEF，PE平面PEF，EF∩PE=E，

∴AB⊥平面PEF．

∵PF平面PEF，

∴AB⊥PF．

依题意得EF=AD=2．

在Rt△PEF中， ，

∴四棱锥P﹣ABCD的侧面积

．

【解析】（1）根据三视图形状可得侧面PDC⊥平面ABCD，结合矩形ABCD中AD⊥CD，由面面垂直的性质得AD⊥侧面PDC．再根据线面垂直的性质，结合PC侧面PDC可证出AD⊥PC；（2）过E作EF⊥AB，垂足为F，连接PF，分别求出侧面积，即得四棱锥P﹣ABCD的侧面积．
【考点精析】根据题目的已知条件，利用空间中直线与直线之间的位置关系的相关知识可以得到问题的答案，需要掌握相交直线：同一平面内，有且只有一个公共点；平行直线：同一平面内，没有公共点；异面直线： 不同在任何一个平面内，没有公共点．