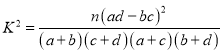题目内容
【题目】已知双曲线C：
的焦点与抛物线
的焦点之间的距离为2,且C的离心率为
，则下列说法正确的有( ).
A.C的渐近线方程为
B.C的标准方程为
C.C的顶点到渐近线的距离为
D.曲线
经过C的一个焦点
【答案】ABD
【解析】
求出抛物线的焦点坐标，设出双曲线的一个焦点坐标，根据两点间距离公式，结合双曲线离心率公式求出双曲线中的
，最后对四个选项逐一判断即可.
设抛物线
的焦点为
，双曲线C的一个焦点坐标为：
，
由题意可知：
，所以有
或
（舍去），
又因为C的离心率为
，所以
.
选项A：因为
，所以C的渐近线方程为
，故本选项说法正确；
选项B：因为，所以C的标准方程为
，故本选项说法正确；
选项C：设C的一个顶点坐标为
，它到渐近线方程为
的距离为：
，根据双曲线和渐近线的对称性可知：C的顶点到渐近线的距离为
，故本选项的说法不正确.
选项D：当
时，
，而
恰好是双曲线的一个焦点，因此本选项的说法正确.
故选：ABD
练习册系列答案
互动英语系列答案
相关题目
【题目】在疫情这一特殊时期，教育行政部门部署了“停课不停学”的行动，全力帮助学生在线学习.复课后进行了摸底考试，某校数学教师为了调查高三学生这次摸底考试的数学成绩与在线学习数学时长之间的相关关系，对在校高三学生随机抽取45名进行调查.知道其中有25人每天在线学习数学的时长是不超过1小时的，得到了如下的等高条形图：
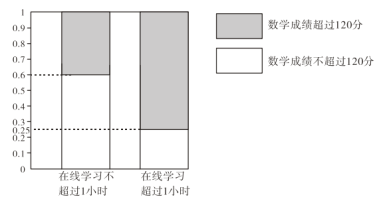
（Ⅰ）是否有
的把握认为“高三学生的这次摸底考试数学成绩与其在线学习时长有关”；
（Ⅱ）将频率视为概率，从全校高三学生这次数学成绩超过120分的学生中随机抽取10人，求抽取的10人中每天在线学习时长超过1小时的人数的数学期望和方差.
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
