题目内容
【题目】设![]() 是椭圆
是椭圆![]()
![]() 的四个顶点,菱形
的四个顶点,菱形![]() 的面积与其内切圆面积分别为
的面积与其内切圆面积分别为![]() ,
, ![]() .椭圆
.椭圆![]() 的内接
的内接![]() 的重心(三条中线的交点)为坐标原点
的重心(三条中线的交点)为坐标原点![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2) ![]() 的面积是否为定值?若是,求出该定值,若不是,请说明理由.
的面积是否为定值?若是,求出该定值,若不是,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(I)由内切圆面积得半径,即为原点到直线PQ的距离,可得![]() ,又四边形PQRS的面积为
,又四边形PQRS的面积为![]() ,从而可得
,从而可得![]() ,解得
,解得![]() 得椭圆方程;
得椭圆方程;
(II)可先求特殊情形下的三角形面积,即![]() 斜率不存在时,C为椭圆的左(右)顶点,求得面积为
斜率不存在时,C为椭圆的左(右)顶点,求得面积为![]() ;当
;当![]() 斜率存在时,设方程为
斜率存在时,设方程为![]() ,代入椭圆方程,并设
,代入椭圆方程,并设![]() ,由韦达定理得
,由韦达定理得![]() ,利用O是
,利用O是![]() 的重心,得
的重心,得![]() 表示出C点坐标,把C点坐标代入椭圆方程求得
表示出C点坐标,把C点坐标代入椭圆方程求得![]() 的关系式为
的关系式为![]() ,由圆锥曲线中的弦长公式求得弦长
,由圆锥曲线中的弦长公式求得弦长![]() ,求出C点到直线AB的距离,从而得三角形ABC的面积,代入刚才的关系式可得
,求出C点到直线AB的距离,从而得三角形ABC的面积,代入刚才的关系式可得![]() ,因此结论为存在.
,因此结论为存在.
试题解析:
(Ⅰ)∵菱形![]() 的面积与其内切圆面积分别为
的面积与其内切圆面积分别为![]() ,
, ![]()
∴![]() ,
,
![]() ,
,
联立解得![]() ,
, ![]() ,
,
故所求椭圆![]() 的方程为
的方程为![]() .
.
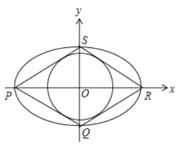
(Ⅱ)当直线![]() 斜率不存在时,
斜率不存在时,
∵![]() 为
为![]() 的重心,∴
的重心,∴![]() 为椭圆的左、右顶点,不妨设
为椭圆的左、右顶点,不妨设![]() ,
,
则直线![]() 的方程为
的方程为![]() ,可得
,可得![]() ,
, ![]() 到直线
到直线![]() 的距离
的距离![]() ,
,
∴![]() .
.
当直线![]() 的斜率存在时,设直线
的斜率存在时,设直线![]() 方程为:
方程为: ![]() ,
, ![]() ,
, ![]() .
.
联立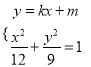 ,得
,得![]() ,
,
则![]()
![]() .
.
即![]() ,
,
![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 的重心,∴
的重心,∴![]() ,
,
∵![]() 点在椭圆
点在椭圆![]() 上,故有
上,故有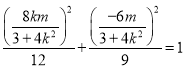 ,
,
化简得![]() .
.
∴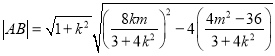
![]() .
.
又点![]() 到直线
到直线![]() 的距离
的距离![]() (
(![]() 是原点到
是原点到![]() 距离的3倍得到).
距离的3倍得到).
∴![]()
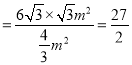 .
.
综上可得, ![]() 的面积为定值
的面积为定值![]() .
.

练习册系列答案
相关题目



