题目内容
在数列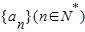 中,a1=1,前n项和Sn满足nSn+1-(n+3)Sn=0.
中,a1=1,前n项和Sn满足nSn+1-(n+3)Sn=0.(1)求{an}的通项公式;
(2)若
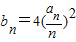 ,求数列{(-1)nbn}的前n项和Tn;
,求数列{(-1)nbn}的前n项和Tn;(3)求证:
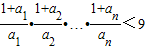 .
.
【答案】分析:(1)方法一:由已知变形得 ,利用“累乘求积”即可得出;
,利用“累乘求积”即可得出;
方法二:利用 得到an的关系式,再利用“累乘求积”即可得出;
得到an的关系式,再利用“累乘求积”即可得出;
(2)根据所求的数列的通项公式的特点,利用等差数列的前n项和公式,可先求出当n为偶数时的Tn,进而即可得出n为奇数时的Tn;
(3)通过构造函数,利用函数的单调性及裂项求和即可证明.
解答:解:(1)方法1:∵ ,且S1=a1=1,
,且S1=a1=1,
∴当n≥2时, ,且S1=1也适合.
,且S1=1也适合.
当n≥2时, ,且a1=1也适合,∴
,且a1=1也适合,∴ .
.
方法2:∵nSn+1-(n+3)Sn=0,∴(n-1)Sn-(n+2)Sn-1=0,
两式相减,得n(Sn+1-Sn)=(n+2)(Sn-Sn-1),即nan+1=(n+2)an,即 .
.
又∵可求得a2=3,∴ 也适合上式.综上,得
也适合上式.综上,得 .
.
当n≥2时, ,且a1=1也适合,
,且a1=1也适合,
∴ .
.
(2) .设
.设 .
.
当n为偶数时,∵ ,
,
∴ .
.
当n为奇数(n≥3)时, ,且T1=c1=-4也适合上式.
,且T1=c1=-4也适合上式.
综上:得 .
.
(3)令f(x)=x-ln(1+x).
当x>0时,∵ ,∴f(x)在(0,+∞)上为增函数,
,∴f(x)在(0,+∞)上为增函数,
∴当x>0时,f(x)>f(0)=0,得ln(1+x)<x.
令 ,得
,得 ,
,
∴ ,
,
∴ ,
,
∴ .
.
点评:数列掌握数列的通项公式、等差数列的前n项和公式、通项公式与前n项和的关系 、“累乘求积”、构造函数并利用函数的单调性及裂项求和是解题的关键.
、“累乘求积”、构造函数并利用函数的单调性及裂项求和是解题的关键.
 ,利用“累乘求积”即可得出;
,利用“累乘求积”即可得出;方法二:利用
 得到an的关系式,再利用“累乘求积”即可得出;
得到an的关系式,再利用“累乘求积”即可得出;(2)根据所求的数列的通项公式的特点,利用等差数列的前n项和公式,可先求出当n为偶数时的Tn,进而即可得出n为奇数时的Tn;
(3)通过构造函数,利用函数的单调性及裂项求和即可证明.
解答:解:(1)方法1:∵
 ,且S1=a1=1,
,且S1=a1=1,∴当n≥2时,
 ,且S1=1也适合.
,且S1=1也适合.当n≥2时,
 ,且a1=1也适合,∴
,且a1=1也适合,∴ .
.方法2:∵nSn+1-(n+3)Sn=0,∴(n-1)Sn-(n+2)Sn-1=0,
两式相减,得n(Sn+1-Sn)=(n+2)(Sn-Sn-1),即nan+1=(n+2)an,即
 .
.又∵可求得a2=3,∴
 也适合上式.综上,得
也适合上式.综上,得 .
.当n≥2时,
 ,且a1=1也适合,
,且a1=1也适合,∴
 .
.(2)
 .设
.设 .
.当n为偶数时,∵
 ,
,∴
 .
.当n为奇数(n≥3)时,
 ,且T1=c1=-4也适合上式.
,且T1=c1=-4也适合上式.综上:得
 .
.(3)令f(x)=x-ln(1+x).
当x>0时,∵
 ,∴f(x)在(0,+∞)上为增函数,
,∴f(x)在(0,+∞)上为增函数,∴当x>0时,f(x)>f(0)=0,得ln(1+x)<x.
令
 ,得
,得 ,
,∴
 ,
,∴
 ,
,∴
 .
.点评:数列掌握数列的通项公式、等差数列的前n项和公式、通项公式与前n项和的关系
 、“累乘求积”、构造函数并利用函数的单调性及裂项求和是解题的关键.
、“累乘求积”、构造函数并利用函数的单调性及裂项求和是解题的关键. 
练习册系列答案
相关题目
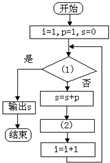 (2012•肇庆二模)在数列{an},a1=1,an+1=an+n,要计算此数列前30项的和,现已给出了该问题算法的程序框图(如图所示),请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能.(1)
(2012•肇庆二模)在数列{an},a1=1,an+1=an+n,要计算此数列前30项的和,现已给出了该问题算法的程序框图(如图所示),请在图中判断框内(1)处和执行框中的(2)处填上合适的语句,使之能完成该题算法功能.(1) 中,a1=1,且
中,a1=1,且 ,计算a2、a3、a4,并猜想
,计算a2、a3、a4,并猜想 =__________.
=__________.