题目内容
下列命题中是假命题的是 .
(A)?m∈R,使f(x)=(m-1)•x m2-4m+3是幂函数;
(B)?φ∈R,函数f(x)=sin(x+φ)都不是偶函数;
(C)?α,β∈R,使cos(α+β)=cosα+cosβ;
(D)?α>0,函数f(x)=ln2x+lnx-a都有零点.
(A)?m∈R,使f(x)=(m-1)•x m2-4m+3是幂函数;
(B)?φ∈R,函数f(x)=sin(x+φ)都不是偶函数;
(C)?α,β∈R,使cos(α+β)=cosα+cosβ;
(D)?α>0,函数f(x)=ln2x+lnx-a都有零点.
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:由幂函数的概念判断(A),举例说明(B)错误,(C)正确;利用换元法求出?a>0,函数f(x)=ln2x+lnx-a都有零点正确.
解答:
解:(A)若f(x)=(m-1)•x m2-4m+3是幂函数,则m=2,此时m2-4m+3=-1,(A)正确;
(B)?φ∈R,函数f(x)=sin(x+φ)都不是偶函数错误,当φ=
时函数为偶函数,(B)错误;
(C)?α,β∈R,使cos(α+β)=cosα+cosβ正确,如α=
,β=-
,(C)正确;
(D)令lnx=t,则方程t2+t-a=0的判别式△=1+4a>0(a>0),则方程t2+t-a=0有两不等实数根t1,t2,由lnx=t1(t2)能求得x的值.
∴?a>0,函数f(x)=ln2x+lnx-a都有零点正确,(D)正确.
∴正确的命题是(A)(C)(D).
故答案为:(A)(C)(D).
(B)?φ∈R,函数f(x)=sin(x+φ)都不是偶函数错误,当φ=
| π |
| 2 |
(C)?α,β∈R,使cos(α+β)=cosα+cosβ正确,如α=
| π |
| 3 |
| π |
| 3 |
(D)令lnx=t,则方程t2+t-a=0的判别式△=1+4a>0(a>0),则方程t2+t-a=0有两不等实数根t1,t2,由lnx=t1(t2)能求得x的值.
∴?a>0,函数f(x)=ln2x+lnx-a都有零点正确,(D)正确.
∴正确的命题是(A)(C)(D).
故答案为:(A)(C)(D).
点评:本题考查了命题的真假判断与应用,考查了函数奇偶性的性质,考查了函数零点的判断,是中档题.

练习册系列答案
相关题目
函数y=esinx(π≤x≤π)的图象大致为( )
A、 |
B、 |
C、 |
D、 |
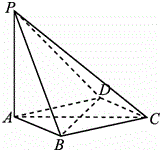 如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.
如图,在四棱椎P-ABCD中,PA⊥平面ABCD,底面ABCD是菱形,AB=2,∠BAD=60°.