题目内容
如图,MA⊥x轴,MA与圆x2+y2=9交于P点,并且|MA|=2|PA|,求点M的轨迹方程,并说明轨迹的形状.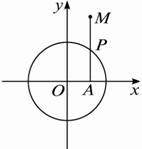
解析:设点M的坐标为(x,y),点P的坐标为(x0,y0),
∵P点在圆x2+y2=9上,
∴x02+y02=9.(*)
∵|MA|=2|PA|,
∴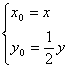 .
.
把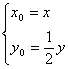 代入(*)式,得x2+
代入(*)式,得x2+![]() =9.?
=9.?
整理得![]() +
+![]() =1,
=1,
故M点的轨迹方程是![]() +
+![]() =1,即M的轨迹是一个椭圆.
=1,即M的轨迹是一个椭圆.
温馨提示:把圆x2+y2=r2上的每个点的横坐标(或纵坐标)不变,纵坐标(或横坐标)伸长或缩短到原来的m(m>0,m≠1)倍,所得的图形是一个椭圆.

练习册系列答案
相关题目
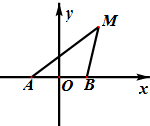 (2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.
(2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.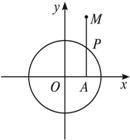
 的取值范围.
的取值范围.