题目内容
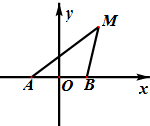 (2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.
(2012•四川)如图,动点M与两定点A(-1,0)、B(1,0)构成△MAB,且直线MA、MB的斜率之积为4,设动点M的轨迹为C.(Ⅰ)求轨迹C的方程;
(Ⅱ)设直线y=x+m(m>0)与y轴交于点P,与轨迹C相交于点Q、R,且|PQ|<|PR|,求
| |PR| | |PQ| |
分析:(Ⅰ)设出点M(x,y),表示出两线的斜率,利用其乘积为4,建立方程化简即可得到点M的轨迹方程;
(Ⅱ)直线y=x+m与4x2-y2-4=0(x≠±1)联立,消元可得3x2-2mx-m2-3=0,结合题设(m>0)可知,m>0且m≠1设Q,R的坐标,求出xR,xQ,利用
=
,即可确定
的取值范围.
(Ⅱ)直线y=x+m与4x2-y2-4=0(x≠±1)联立,消元可得3x2-2mx-m2-3=0,结合题设(m>0)可知,m>0且m≠1设Q,R的坐标,求出xR,xQ,利用
| |PR| |
| |PQ| |
| xR |
| xQ |
| |PR| |
| |PQ| |
解答:解:(Ⅰ)设M(x,y),则kMA=
,kMB=
∵直线MA、MB的斜率之积为4,
∴
×
=4
∴4x2-y2-4=0
又x=±1时,必有一个斜率不存在,故x≠±1
综上点M的轨迹方程为4x2-y2-4=0(x≠±1)
(Ⅱ)直线y=x+m与4x2-y2-4=0(x≠±1)联立,消元可得3x2-2mx-m2-4=0①
∴△=16m2+48>0
当1或-1是方程①的根时,m的值为1或-1,结合题设(m>0)可知,m>0且m≠1
设Q,R的坐标分别为(xQ,yQ),(xR,yR),
∵|PQ|<|PR|,∴xR=
,xQ=
,
∴
=
=
=1-
∵m>0且m≠1
∴1+
>1,且1+
≠4
∴1<1-
<3,且1-
≠
∴
的取值范围是(1,
)∪(
,3)
| y |
| x+1 |
| y |
| x-1 |
∵直线MA、MB的斜率之积为4,
∴
| y |
| x+1 |
| y |
| x-1 |
∴4x2-y2-4=0
又x=±1时,必有一个斜率不存在,故x≠±1
综上点M的轨迹方程为4x2-y2-4=0(x≠±1)
(Ⅱ)直线y=x+m与4x2-y2-4=0(x≠±1)联立,消元可得3x2-2mx-m2-4=0①
∴△=16m2+48>0
当1或-1是方程①的根时,m的值为1或-1,结合题设(m>0)可知,m>0且m≠1
设Q,R的坐标分别为(xQ,yQ),(xR,yR),
∵|PQ|<|PR|,∴xR=
m+2
| ||
| 3 |
m-2
| ||
| 3 |
∴
| |PR| |
| |PQ| |
| -xR |
| xQ |
-
| ||||
|
| 2 | ||||
1-2
|
∵m>0且m≠1
∴1+
| 3 |
| m2 |
| 3 |
| m2 |
∴1<1-
| 2 | ||||
1-2
|
| 2 | ||||
1-2
|
| 5 |
| 3 |
∴
| |PR| |
| |PQ| |
| 5 |
| 3 |
| 5 |
| 3 |
点评:本题以斜率为载体,考查直线、双曲线、轨迹方程的求解,考查思维能力,运算能力,考查思维的严谨性.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
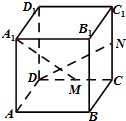 (2012•四川)如图,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成的角的大小是
(2012•四川)如图,在正方体ABCD-A1B1C1D1中,M、N分别是CD、CC1的中点,则异面直线A1M与DN所成的角的大小是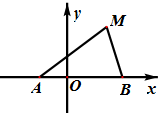 (2012•四川)如图,动点M到两定点A(-1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.
(2012•四川)如图,动点M到两定点A(-1,0)、B(2,0)构成△MAB,且∠MBA=2∠MAB,设动点M的轨迹为C.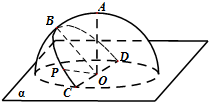 (2012•四川)如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( )
(2012•四川)如图,半径为R的半球O的底面圆O在平面α内,过点O作平面α的垂线交半球面于点A,过圆O的直径CD作平面α成45°角的平面与半球面相交,所得交线上到平面α的距离最大的点为B,该交线上的一点P满足∠BOP=60°,则A、P两点间的球面距离为( ) (2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上.
(2012•四川)如图,在三棱锥P-ABC中,∠APB=90°,∠PAB=60°,AB=BC=CA,点P在平面ABC内的射影O在AB上.