题目内容
下图中的三角形称为谢宾斯基(Sierpinski)三角形.这些三角形中的着色与未着色的三角形的个数具有一定的规律.按图(1)、(2)、(3)、(4)四个三角形的规律继续构建三角形,设第n个三角形中包含f(n)个未着色三角形.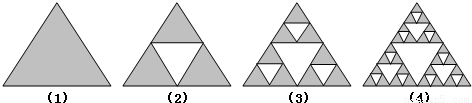
(Ⅰ)求出f(5)的值;
(Ⅱ)写出f(n+1)与f(n)之间的关系式,并由此求出f(n)的表达式;
(Ⅲ)设
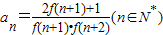 ,数列{an}的前n项和为Sn,求证:
,数列{an}的前n项和为Sn,求证: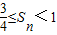 .
.
【答案】分析:(Ⅰ)由图知f(1)=0,f(2)=1,f(3)=4,f(4)=13,从而可得f(5)的值;
(Ⅱ)方法1:由f(2)-f(1)=1,f(3)-f(2)=3,f(4)-f(3)=9,f(5)-f(4)=27,归纳得:f(n+1)-f(n)=3n-1(n∈N*),利用叠加法,可求f(n)的表达式;
方法2:f(2)=3f(1)+1,f(3)=3f(2)+1,f(4)=3f(3)+1,f(5)=3f(4)+1,归纳得:f(n+1)=3f(n)+1(n∈N*),从而可证数列 是首项为
是首项为 ,公比为3的等比数列,即可求f(n)的表达式;
,公比为3的等比数列,即可求f(n)的表达式;
(Ⅲ)由 ,得
,得 ,进而可求数列{an}的前n项和为Sn,由此可证结论成立.
,进而可求数列{an}的前n项和为Sn,由此可证结论成立.
解答:解:(Ⅰ)由图知f(1)=0,f(2)=1,f(3)=1+3=4,f(4)=1+3+9=13,f(5)=1+3+9+27=40
(Ⅱ)方法1:由f(2)-f(1)=1,f(3)-f(2)=3,f(4)-f(3)=9,f(5)-f(4)=27
归纳得:f(n+1)-f(n)=3n-1(n∈N*)∴f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]= ,
,
方法2:f(2)=3f(1)+1,f(3)=3f(2)+1,f(4)=3f(3)+1,f(5)=3f(4)+1
归纳得:f(n+1)=3f(n)+1(n∈N*)
由f(n+1)=3f(n)+1,可得
∴数列 是首项为
是首项为 ,公比为3的等比数列
,公比为3的等比数列
∴ ,即
,即
(Ⅲ)由 ,得
,得
∴ .
.
∵3n+1≥9,∴ ,
,
∴ .
.
点评:本题考查归纳推理,考查数列通项的求解,考查数列的求和,考查学生阅读分析的能力,综合性强.
(Ⅱ)方法1:由f(2)-f(1)=1,f(3)-f(2)=3,f(4)-f(3)=9,f(5)-f(4)=27,归纳得:f(n+1)-f(n)=3n-1(n∈N*),利用叠加法,可求f(n)的表达式;
方法2:f(2)=3f(1)+1,f(3)=3f(2)+1,f(4)=3f(3)+1,f(5)=3f(4)+1,归纳得:f(n+1)=3f(n)+1(n∈N*),从而可证数列
 是首项为
是首项为 ,公比为3的等比数列,即可求f(n)的表达式;
,公比为3的等比数列,即可求f(n)的表达式;(Ⅲ)由
 ,得
,得 ,进而可求数列{an}的前n项和为Sn,由此可证结论成立.
,进而可求数列{an}的前n项和为Sn,由此可证结论成立.解答:解:(Ⅰ)由图知f(1)=0,f(2)=1,f(3)=1+3=4,f(4)=1+3+9=13,f(5)=1+3+9+27=40
(Ⅱ)方法1:由f(2)-f(1)=1,f(3)-f(2)=3,f(4)-f(3)=9,f(5)-f(4)=27
归纳得:f(n+1)-f(n)=3n-1(n∈N*)∴f(n)=f(1)+[f(2)-f(1)]+[f(3)-f(2)]+…+[f(n)-f(n-1)]=
 ,
,
方法2:f(2)=3f(1)+1,f(3)=3f(2)+1,f(4)=3f(3)+1,f(5)=3f(4)+1
归纳得:f(n+1)=3f(n)+1(n∈N*)
由f(n+1)=3f(n)+1,可得

∴数列
 是首项为
是首项为 ,公比为3的等比数列
,公比为3的等比数列∴
 ,即
,即
(Ⅲ)由
 ,得
,得
∴
 .
.∵3n+1≥9,∴
 ,
,∴
 .
.点评:本题考查归纳推理,考查数列通项的求解,考查数列的求和,考查学生阅读分析的能力,综合性强.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目



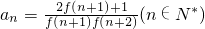 ,数列{an}的前n项和为Sn,求证:
,数列{an}的前n项和为Sn,求证: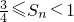 .
.