Question

图中的三角形称为谢宾斯基（Sierpinski）三角形．在下图中，将第1个三角形的三边中点为顶点的三角形着色，将第k（k∈N^*）个图形中的每个未着色三角形的三边中点为顶点的三角形着色，得到第k+1个图形，这样这些图形中着色三角形的个数依次构成一个数列{a_n}，则数列{a_n}的通项公式为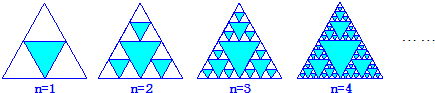

 

．

Answer 1

分析：先根据图形求出前后两图的递推关系，然后利用叠加法进行求解，即可求出数列的通项公式．

解答：解：根据图形可知a₁=1，a_n+1-a_n=3ⁿ
当n≥2时
a_n=a₁+（a₂-a₁）+（a₃-a₂）+…+（a_n-a_n-1）
=1+3+3²+…3^n-1
=

3n-1

2

故答案为：an=

3n-1

2

．

点评：本题主要考查了数列的应用，以及识图能力和运算推理能力，属于中档题．