题目内容
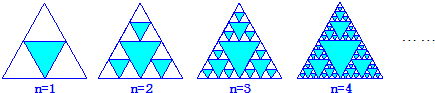
图中的三角形称为谢宾斯基(Sierpinski)三角形.在下图4个三角形中,着色三角形的个数依次构成一个数列的前4项,则这个数列的一个通项公式为

an=
| 3n-1 |
| 2 |
an=
| 3n-1 |
| 2 |

分析:先根据图形求出前后两图的递推关系,然后利用叠加法进行求解,再利用等比数例,求出数列的通项公式.
解答:解:根据图形可知 a1=1,an+1-an=3n
当n≥2时
an=a1+(a2-a1)+(a3-a2)+…(an-an-1)
=1+3+32+…+3n-1
=
故答案为:
.
当n≥2时
an=a1+(a2-a1)+(a3-a2)+…(an-an-1)
=1+3+32+…+3n-1
=
| 3n-1 |
| 2 |
故答案为:
| 3n-1 |
| 2 |
点评:本题主要考查了等比数列的求和,数列中的叠加法求通项,以及识图能力和运算推理能力.

练习册系列答案
相关题目