题目内容

已知f(θ)=
1+cosθ-sinθ
1-sinθ-cosθ
+
1-cosθ-sinθ
1-sinθ+cosθ
．
（1）化简f（θ）；
（2）求使f（θ）=4的最小正角θ．
分析：（1）利用二倍角公式对原式进行化简整理求得答案．
（2）把（1）中求得函数解析式代入f（θ）=4求得答案．
解答：解：（1）
1+cosθ-sinθ
1-sinθ-cosθ
=
2cos  2
θ
2
 -2sin
θ
2
cos
θ
2
2sin2
θ
2
-2sin
θ
2
cos
θ
2
=-cot
θ
2

∴f(θ)=
1+cosθ-sinθ
1-sinθ-cosθ
+
1-cosθ-sinθ
1-sinθ+cosθ
.=-cot
θ
2
-tan
θ
2
=-2cscθ
（2）f（θ）=-2cscθ=4
∴cscθ=-2，sinθ=-
1
2

∴满足条件的最小正角
7
6
π
点评：本题主要考查了运用二倍角公式进行化简求值．考查了学生对三角函数基本公式的理解和记忆．
练习册系列答案
相关题目
已知F（c，0）是椭圆
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点，以坐标原点O为圆心，a为半径作圆P，过F垂直于x轴的直线与圆P交于A，B两点，过点A作圆P的切线交x轴于点M．若直线l过点M且垂直于x轴，则直线l的方程为
 
；若|OA|=|AM|，则椭圆的离心率等于
 
．
已知F（c，0）是双曲线C：
x2
a2
-
y2
b2
=1(a＞0，b＞0)的右焦点，若双曲线C的渐近线与圆E：(x-c)2+y2=
1
2
c2相切，则双曲线C的离心率为
2
2
．
已知f(α)=
1+cos2α
1
tan
α
2
-tan
α
2
，α∈(0，
π
2
)，则f（α）取得最大值时α的值是（　　）
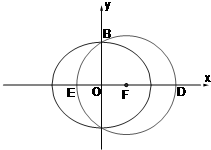精英家教网如图，已知F（c，0）是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点；⊙F：（x-c）2+y2=a2与x轴交于D，E两点，其中E是椭圆C的左焦点．
（1）求椭圆C的离心率；
（2）设⊙F与y轴的正半轴的交点为B，点A是点D关于y轴的对称点，试判断直线AB与⊙F的位置关系；
（3）设直线BF与⊙F交于另一点G，若△BGD的面积为4
3
，求椭圆C的标准方程．
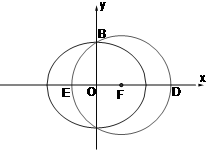精英家教网如图，已知F（c，0）是椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的右焦点；⊙F：（x-c）2+y2=a2与x轴交于D，E两点，其中E是椭圆C的左焦点．
（1）求椭圆C的离心率；
（2）设⊙F与y轴的正半轴的交点为B，点A是点D关于y轴的对称点，试判断直线AB与⊙F的位置关系；
（3）设直线AB与椭圆C交于另一点G，若△BGD的面积为
24
6
13
c，求椭圆C的标准方程．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网