题目内容
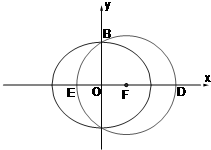 如图,已知F(c,0)是椭圆C:
如图,已知F(c,0)是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
(1)求椭圆C的离心率;
(2)设⊙F与y轴的正半轴的交点为B,点A是点D关于y轴的对称点,试判断直线AB与⊙F的位置关系;
(3)设直线BF与⊙F交于另一点G,若△BGD的面积为4
| 3 |
分析:(1)将椭圆左焦点坐标代入圆F的方程,算出a=2c,即可得出椭圆C的离心率;
(2)根据椭圆基本量的平方关系算出圆F与y轴正半轴的交点为椭圆的上顶点,进而得到B(0,
c).再求出D点与A点的坐标,利用直线的斜率公式算出直线AB、BF的斜率,证出直线AB与半径BF相垂直,可得AB与⊙F相切;
(3)利用三角形中线的性质与三角形面积公式,得到△BGD的面积关于c的表达式,解出c2=2,从而得出a2、b2的值,可得椭圆C的标准方程.
(2)根据椭圆基本量的平方关系算出圆F与y轴正半轴的交点为椭圆的上顶点,进而得到B(0,
| 3 |
(3)利用三角形中线的性质与三角形面积公式,得到△BGD的面积关于c的表达式,解出c2=2,从而得出a2、b2的值,可得椭圆C的标准方程.
解答:解:(1)∵圆F:(x-c)2+y2=a2过椭圆C的左焦点,
∴将(-c,0)代入圆F的方程,得4c2=a2,可得a=2c.
因此,椭圆C的离心率e=
=
;
(2)在方程(x-c)2+y2=a2中令x=0,得y2=a2-c2=b2,
∴⊙F与y轴的正半轴的交点为B(0,b),可知点B为椭圆的上顶点,
又∵a=2c,∴b=
=
c,故B(0,
c),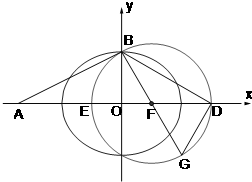
在圆F的方程中令y=0,可得点D坐标为(3c,0),
∴D关于y轴的对称点是A(-3c,0),
由此可得直线AB的斜率kAB=
=
,
而直线FB的斜率kFB=
=-
,
∵kAB•kFB=-1,直线AB与半径BF相垂直,
∴直线AB与⊙F相切.
(3)∵DF是△BDG的中线,
∴S△BDG=2S△BFD=|FD|•|OB|=2c•
c=4
,
解之得c2=2,从而得出a2=4c2=8,b2=3c2=6,
∴所求椭圆的标准方程为
+
=1.
∴将(-c,0)代入圆F的方程,得4c2=a2,可得a=2c.
因此,椭圆C的离心率e=
| c |
| a |
| 1 |
| 2 |
(2)在方程(x-c)2+y2=a2中令x=0,得y2=a2-c2=b2,
∴⊙F与y轴的正半轴的交点为B(0,b),可知点B为椭圆的上顶点,
又∵a=2c,∴b=
| a2-c2 |
| 3 |
| 3 |

在圆F的方程中令y=0,可得点D坐标为(3c,0),
∴D关于y轴的对称点是A(-3c,0),
由此可得直线AB的斜率kAB=
| ||
| 3c |
| ||
| 3 |
而直线FB的斜率kFB=
| ||
| -c |
| 3 |
∵kAB•kFB=-1,直线AB与半径BF相垂直,
∴直线AB与⊙F相切.
(3)∵DF是△BDG的中线,
∴S△BDG=2S△BFD=|FD|•|OB|=2c•
| 3 |
| 3 |
解之得c2=2,从而得出a2=4c2=8,b2=3c2=6,
∴所求椭圆的标准方程为
| x2 |
| 8 |
| y2 |
| 6 |
点评:本题着重考查了圆的标准方程、直线与圆的位置关系、椭圆的标准方程与简单几何性质等知识,考查了三角形的中线的性质与三角形面积的求法,属于中档题.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
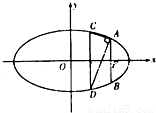
 (2012•潍坊二模)如图,已知F(2,0)为椭圆
(2012•潍坊二模)如图,已知F(2,0)为椭圆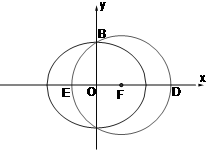 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆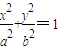 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.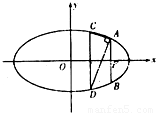
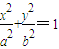 (a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.
(a>b>0)的右焦点,AB为椭圆的通径(过焦点且垂直于长轴的弦),线段OF的垂直平分线与椭圆相交于两点C、D,且∠CAD=90°.