题目内容
已知f(α)=
,α∈(0,
),则f(α)取得最大值时α的值是( )
| 1+cos2α | ||||||
|
| π |
| 2 |
分析:利用正切函数的半角公式与余弦函数的二倍角公式可将f(α)化简为f(α)=
sin2α,又α∈(0,
),从而可得f(α)取得最大值时α的值.
| 1 |
| 2 |
| π |
| 2 |
解答:解:∵tan
=
=
,
∴
-tan
=
-
=
,又1+cos2α=2cos2α,
∴f(α)=
=sinα•cosα=
sin2α,
又α∈(0,
),
∴α=
时,f(α)取得最大值
.
故选D.
| α |
| 2 |
| sinα |
| 1+cosα |
| 1-cosα |
| sinα |
∴
| 1 | ||
tan
|
| α |
| 2 |
| 1+cosα |
| sinα |
| 1-cosα |
| sinα |
| 2cosα |
| sinα |
∴f(α)=
| 2cos2α•sinα |
| 2cosα |
| 1 |
| 2 |
又α∈(0,
| π |
| 2 |
∴α=
| π |
| 4 |
| 1 |
| 2 |
故选D.
点评:本题考查三角函数的化简求值,掌握正切函数的半角公式与余弦函数的二倍角公式是关键,考查应用三角函数公式解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
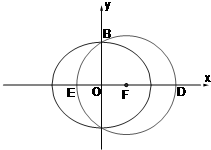 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆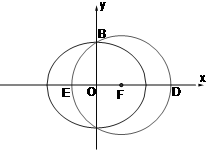 如图,已知F(c,0)是椭圆
如图,已知F(c,0)是椭圆