题目内容
10.已知数列{an}的中,a2=2,a2n=an+1,a2n+1=n-an,则{an}的前100项和为1287.分析 由已知得a1=1,a2n+1+a2n=n+1,由此能求出{an}的前100项和.
解答 解:∵a2n=an+1,a2n+1=n-an,
∴a2=a1+1=2,解得a1=1,
∴an=a2n-1,an=n-a2n+1,∴a2n+1+a2n=n+1,
∴a1+(a2+a3)+(a4+a5)+…+(a98+a99)=1+2+3+…+50=1275,
a100=a50+1=a25+2=12-a12+2=14-a6-1=13-a3-1=12-1+a1=12,
∴{an}的前100项和S100=1275+12=1287.
故答案为:1287.
点评 本题考查数列的前100项和的求法,是基础题,解题时要认真审题,注意数列的性质的合理运用.

练习册系列答案
相关题目
1.圆O中,弦AB满足|AB|=2,则$\overrightarrow{AB}$•$\overrightarrow{AO}$=( )
| A. | 2 | B. | 1 | C. | $\frac{1}{2}$ | D. | 4 |
15.若函数y=2sin(x+θ)的图象向右平移$\frac{π}{6}$个单位,再向上平移2个单位后,它的一条对称轴是$x=\frac{π}{4}$,则θ的一个可能的值是( )
| A. | $\frac{5π}{12}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{12}$ |
2.若a=0.30.3,b=0.33,c=log0.33,则a,b,c的大小顺序是( )
| A. | a<b<c | B. | c<a<b | C. | c<b<a | D. | b<c<a |
19.下列是映射的是( )


| A. | (1)(2)(3) | B. | (1)(2)(5) | C. | (1)(3)(5) | D. | (1)(2)(3)(5) |
20.不等式|$\frac{2-x}{3}$|>1的解集是( )
| A. | (-∞,-5)∪(-1,+∞) | B. | (-∞,-5)∪(1,+∞) | C. | (-∞,-1)∪(5,+∞) | D. | (-∞,1)∪(5,+∞) |
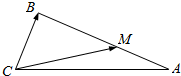 如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.
如图,在△ABC中,|$\overrightarrow{CA}$|=6,|$\overrightarrow{CB}$|=3,M为线段AB上的一点,且|$\overrightarrow{CM}$|=x•$\overrightarrow{CA}$+y•$\overrightarrow{CB}$,$\overrightarrow{BM}$=2$\overrightarrow{MA}$.