题目内容
4．等差数列{an}的前n项和为Sn，已知a10=30，S5=80．（1）求通项an；
（2）若Sn=242，求n．
分析 （1）由等差数列的求和公式和通项公式可得首项和公差的方程组，解方程组可得通项公式；
（2）由题意和求和公式可得n的方程，解关于n的方程可得n值．
解答 解：（1）设等差数列{an}的公差为d，
∵a10=30，S5=80，
∴a1+9d=30，5a1+$\frac{5×4}{2}$d=80，
解得a1=12，d=2，
∴通项an=12+2（n-1）=2n+10；
（2）∵Sn=12n+$\frac{n（n-1）}{2}$×2=242，
解关于n的方程可得n=11或n=-22（舍去），
∴n的值为11
点评 本题考查等差数列的通项公式和求和公式，属基础题．
练习册系列答案
小博士期末闯关100分系列答案
名校名师培优作业本加核心试卷系列答案
相关题目
19．若sinα=$-\frac{1}{2}$，α∈（-$\frac{π}{2}$，0），则tanα等于（ ）
| A． | -$\frac{1}{2}$ | B． | -$\frac{\sqrt{3}}{2}$ | C． | -$\sqrt{3}$ | D． | -$\frac{\sqrt{3}}{3}$ |
16．
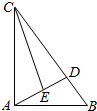如图所示，在Rt△ABC中，∠BAC=90°，AB=2，BC=4，BD=$\frac{1}{4}$BC，E是AD的中点，则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是（ ）
如图所示，在Rt△ABC中，∠BAC=90°，AB=2，BC=4，BD=$\frac{1}{4}$BC，E是AD的中点，则$\overrightarrow{CE}$$•\overrightarrow{AB}$的值是（ ）| A． | 3 | B． | $\sqrt{3}$ | C． | 2$\sqrt{3}$ | D． | $\frac{3}{2}$ |