题目内容
5.在极坐标系中,圆ρ=2与极轴交于点A,与直线θ=$\frac{π}{3}$(ρ∈R)交于点B,C,则△ABC的周长为( )| A. | 6$+2\sqrt{2}$ | B. | 6$+2\sqrt{3}$ | C. | 6$+\sqrt{2}$ | D. | 6$+\sqrt{3}$ |
分析 由题意可得△AOB为等边三角形,∠AOC=$\frac{2π}{3}$,由余弦定理可得AC的值,可得△ABC的周长.
解答 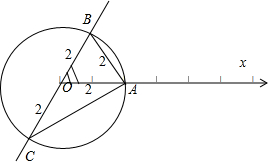 解:如图所示:由题意可得△AOB为等边三角形,∠AOC=$\frac{2π}{3}$,
解:如图所示:由题意可得△AOB为等边三角形,∠AOC=$\frac{2π}{3}$,
由余弦定理可得AC=$\sqrt{{OA}^{2}{+OC}^{2}-2OA•OC•cos\frac{2π}{3}}$=$\sqrt{4+4-2×2×2×(-\frac{1}{2})}$=2$\sqrt{3}$,
∴△ABC的周长为 AB+BC+AC=2+4+2$\sqrt{3}$=6+2$\sqrt{3}$,
故选:B.
点评 本题主要考查简单曲线的极坐标方程,余弦定理的应用,属于基础题.

练习册系列答案
 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
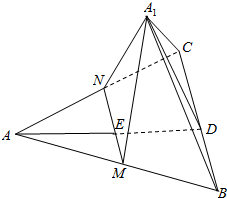 如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.
如图,AD为△ABC的边BC上的高,E在AD上,且ED=2AE,过E作直线MN∥BC,分别交AB,AC于M,N点,将△AMN沿MN折起到A1MN,使二面角A1-MN-C为60°,求证:平面A1MN⊥平面A1BC.