题目内容
15.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>0.b>0)上任意一点M(非短轴的端点)与短轴的两个端点 B1、B2的连线交x轴于N和K,求证:|ON|•|OK|为定值.分析 设M(x0,y0),代入椭圆方程可得$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,变形为${b}^{2}{x}_{0}^{2}$=${a}^{2}({b}^{2}-{y}_{0}^{2})$.直线B1N的方程为:$y=\frac{{y}_{0}-b}{{x}_{0}}x+b$,可得N.同理可得K.即可证明.
解答 证明:设M(x0,y0),则$\frac{{x}_{0}^{2}}{{a}^{2}}+\frac{{y}_{0}^{2}}{{b}^{2}}=1$,化为${b}^{2}{x}_{0}^{2}$=${a}^{2}({b}^{2}-{y}_{0}^{2})$.
直线B1N的方程为:$y=\frac{{y}_{0}-b}{{x}_{0}}x+b$,可得N$(\frac{b{x}_{0}}{b-{y}_{0}},0)$.
直线B2K的方程为:$y=\frac{{y}_{0}+b}{{x}_{0}}x-b$,可得K$(\frac{b{x}_{0}}{{y}_{0}+b},0)$.
∴|ON|•|OK|=$\frac{b{x}_{0}}{b-{y}_{0}}$$•\frac{b{x}_{0}}{{y}_{0}+b}$=$\frac{{b}^{2}{x}_{0}^{2}}{{b}^{2}-{y}_{0}^{2}}$=$\frac{{a}^{2}({b}^{2}-{y}_{0}^{2})}{{b}^{2}-{y}_{0}^{2}}$=a2,为定值.
点评 本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.在极坐标系中,圆ρ=2与极轴交于点A,与直线θ=$\frac{π}{3}$(ρ∈R)交于点B,C,则△ABC的周长为( )
| A. | 6$+2\sqrt{2}$ | B. | 6$+2\sqrt{3}$ | C. | 6$+\sqrt{2}$ | D. | 6$+\sqrt{3}$ |
6.已知数列{an}的通项公式为an =n2+1,则该数列的第6项是( )
| A. | 37 | B. | 36 | C. | 26 | D. | 7 |
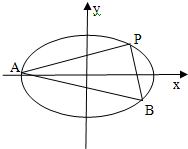 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.