题目内容
14.已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的离心率为$\frac{\sqrt{2}}{2}$,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为1.(Ⅰ)求椭圆C的标准方程;
(Ⅱ)C上是否存在点P,使得当l绕F转到某一位置时,有$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$成立?若存在,求出所有的P的坐标与l的方程;若不存在,说明理由.
分析 (I)运用椭圆的离心率公式和点到直线的距离公式,计算即可得到a,b,进而得到椭圆方程;
(II)设A(x1,y1),B(x2,y2),不妨设$l:x=my+\sqrt{2}$,代入椭圆方程,运用韦达定理和点满足椭圆方程,运用向量共线的坐标表示,化简整理,即可得到m,进而得到直线方程和P的坐标.
解答 解:(I)离心率为$\frac{\sqrt{2}}{2}$,即有e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$,
F(c,0),直线l:y=x-c,
由坐标原点到l的距离为1,
则$\frac{|c|}{{\sqrt{2}}}=1$,解得$c=\sqrt{2}$.
所以$a=2,b=c=\sqrt{2}$,
则椭圆C的标准方程为$\frac{x^2}{4}+\frac{y^2}{2}=1$;
(II)椭圆C的方程为x2+2y2=4,设A(x1,y1),B(x2,y2),
由题意知l的斜率为一定不为0,
故不妨设$l:x=my+\sqrt{2}$,
代入椭圆的方程中整理得$({m^2}+2){y^2}+2\sqrt{2}my-2=0$,
显然△>0.
由韦达定理有:${y_1}+{y_2}=-\frac{{2\sqrt{2}m}}{{{m^2}+2}}$,${y_1}{y_2}=-\frac{2}{{{m^2}+2}}$….①
假设存在点P,使$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$成立,
则点P的坐标为(x1+x2,y1+y2),
因为点P在椭圆上,即${({x_1}+{x_2})^2}+2{({y_1}+{y_2})^2}=4$.
整理得$({x_1}^2+2{y_1}^2)+({x_2}^2+2{y_2}^2)+2({x_1}{x_2}+2{y_1}{y_2})=4$.
又A,B在椭圆上,即${x_1}^2+2{y_1}^2=4,{x_2}^2+2{y_2}^2=4$.
故x1x2+2y1y2+2=0…②,
将${x_1}{x_2}=(m{y_1}+\sqrt{2})(m{y_2}+\sqrt{2})={m^2}{y_1}{y_2}+\sqrt{2}m({y_1}+{y_2})+2$及①代入②
解得m2=2,
所以y1+y2=±1,x1+x2=$-\frac{{2\sqrt{2}{m^2}}}{{{m^2}+2}}+2\sqrt{2}$=$\sqrt{2}$,
即P($\sqrt{2}$,±1).
则当$m=\sqrt{2}$时,$P(\sqrt{2},-1),l:x=\sqrt{2}y+\sqrt{2}$;
当$m=-\sqrt{2}$时,$P(\sqrt{2},1),l:x=-\sqrt{2}y+\sqrt{2}$.
点评 本题考查椭圆的方程和性质,考查直线方程和椭圆方程联立,运用韦达定理,同时考查向量共线的坐标表示,以及直线方程的知识,属于中档题.

 阅读快车系列答案
阅读快车系列答案| A. | 有且只有一个 | B. | 有且只有两个 | C. | 有且只有三个 | D. | 有且只有四个 |
| A. | 0 | B. | -1 | C. | ±1 | D. | 1 |
| A. | 6$+2\sqrt{2}$ | B. | 6$+2\sqrt{3}$ | C. | 6$+\sqrt{2}$ | D. | 6$+\sqrt{3}$ |
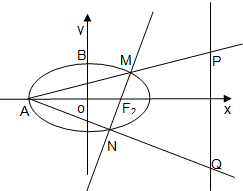 如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.
如图所示,设F1、F2是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点,A、B分别为其左顶点与上顶点,椭圆的离心率e=$\frac{1}{2}$,原点到过点A、B的直线的距离为$\frac{{2\sqrt{21}}}{7}$.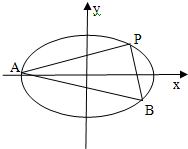 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,1),且两焦点与短轴的一个端点构成等腰直角三角形.