题目内容
1．若集合M={x|x2＞4}，N={x|1＜x≤3}，则N∩（∁RM）=（ ）| A． | {x|1＜x≤2} | B． | {x|-2≤x≤2} | C． | {x|-2≤x＜1} | D． | {x|-2≤x≤3} |
分析 求出集合M，然后进行集合的补集、交集运算即可．
解答 解：M={x|x＞2，或x＜-2}，N={x|1＜x≤3}；
∴∁RM={-2≤x≤2}；
∴N∩（∁RM）={x|1＜x≤2}．
故选A．
点评 考查解一元二次不等式，描述法表示集合，以及补集、交集的运算．
练习册系列答案
黄冈冠军课课练系列答案
相关题目
12．
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）
如图，网格纸上小正方形的边长为1，粗实线画出的是某多面体的三视图，则该多面体的各条棱中，最长的棱的长度为（ ）| A． | 2$\sqrt{2}$ | B． | $\sqrt{6}$ | C． | 3 | D． | 2$\sqrt{3}$ |
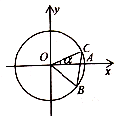如图，圆O与x轴的正半轴的交点为A，点C、B在圆O上，且点C位于第一象限，点B的坐标为（$\frac{12}{13}$，-$\frac{5}{13}$），∠AOC=α，若|BC|=1，则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$．
13．直线y=ax+b通过第一、二、三象限，则圆（x+a）2+（y+b）2=r2（r＞0）的圆心位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |
10．若函数f（x）=a+|x|+log2（x2+2）有且只有一个零点，则实数a的值是（ ）
| A． | -2 | B． | -1 | C． | 0 | D． | 2 |