题目内容
9.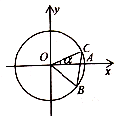 如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
如图,圆O与x轴的正半轴的交点为A,点C、B在圆O上,且点C位于第一象限,点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),∠AOC=α,若|BC|=1,则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$的值为$\frac{5}{13}$.
分析 根据三角函数的定义,结合三角函数的辅助角公式进行化简即可得到结论.
解答 解:∵点B的坐标为($\frac{12}{13}$,-$\frac{5}{13}$),设∠A0B=θ
∴sin(2π-θ)=-$\frac{5}{13}$,cos(2π-θ)=$\frac{12}{13}$,
即sinθ=$\frac{5}{13}$,cosθ=$\frac{12}{13}$,
∵∠AOC=α,若|BC|=1,∴θ+α=$\frac{π}{3}$,
则α=$\frac{π}{3}$-θ,
则$\sqrt{3}$cos2$\frac{α}{2}$-sin$\frac{α}{2}$cos$\frac{α}{2}$-$\frac{\sqrt{3}}{2}$=$\frac{\sqrt{3}}{2}$cosα-$\frac{1}{2}$sinα=cos(α+$\frac{π}{6}$)=cos($\frac{π}{3}$-θ+$\frac{π}{6}$)=cos($\frac{π}{2}-θ$)
=sinθ=$\frac{5}{13}$,
故答案为:$\frac{5}{13}$
点评 本题主要考查三角函数的化简和求值,利用三角函数的定义以及三角函数的辅助角公式是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19.函数f(x)=$\frac{1}{2}$(1+cos2x)sin2x,x∈R是( )
| A. | 最小正周期为π的奇函数 | B. | 最小正周期为$\frac{π}{2}$的奇函数 | ||
| C. | 最小正周期为π的偶函数 | D. | 最小正周期为$\frac{π}{2}$的偶函数 |
4.数列{an}的前n项和Sn=2n2-3n(n∈N+),若p-q=5,则ap-aq=( )
| A. | 10 | B. | 15 | C. | -5 | D. | 20 |
14.设变量x,y满足约束条件$\left\{\begin{array}{l}y≥x\\ x+3y≤4\\ x≥-2\end{array}\right.$则z=|x-3y|的取值范围为( )
| A. | [2,8] | B. | [0,8] | C. | [4,8] | D. | [0,4] |
1.若集合M={x|x2>4},N={x|1<x≤3},则N∩(∁RM)=( )
| A. | {x|1<x≤2} | B. | {x|-2≤x≤2} | C. | {x|-2≤x<1} | D. | {x|-2≤x≤3} |
18.设△ABC的内角A,B,C所对的边a,b,c成等比数列,则$\frac{sinA+cosA•tanC}{sinB+cosB•tanC}$的取值范围是( )
| A. | (0,+∞) | B. | $({\frac{{\sqrt{5}-1}}{2},+∞})$ | C. | $({0,\frac{{\sqrt{5}+1}}{2}})$ | D. | $({\frac{{\sqrt{5}-1}}{2},\frac{{\sqrt{5}+1}}{2}})$ |
19.已知F1、F2为双曲线C:$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的左、右焦点,P为双曲线C右支上一点,且PF2⊥F1F2,PF1与y轴交于点Q,点M满足$\overrightarrow{{F}_{1}M}$=3$\overrightarrow{M{F}_{2}}$,若MQ⊥PF1,则双曲线C的离心率为( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{2}+\sqrt{3}}{2}$ | D. | $\frac{\sqrt{2}+\sqrt{6}}{2}$ |