题目内容
已知双曲线与椭圆 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求:
,求:
(1)双曲线的标准方程;
(2)双曲线的渐近线方程.
解:(1)∵椭圆焦点为F(±4,0),离心率为e= ,而双曲线与椭圆
,而双曲线与椭圆 共焦点,
共焦点,
∴双曲线的焦点为F(±4,0),又它们的离心率之和为 ,设该双曲线的离心率为e,则e+
,设该双曲线的离心率为e,则e+ =
= ,
,
∴e=2,即 =2,而c=4,
=2,而c=4,
∴a=2,b=2 .
.
∴双曲线方程为: -
-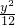 =1;
=1;
(2)∵双曲线方程为: -
-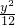 =1,
=1,
∴其渐近线方程为y=±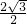 x,
x,
即y= x或y=-
x或y=- x.
x.
分析:(1)由题意可知双曲线的焦点在x轴,并求得焦点为F(±4,0),离心率为2,从而c=4,a=2,b=2 ;
;
(2)利用双曲线方程即可写出其渐近线方程.
点评:本题考查双曲线的标准方程与双曲线的简单性质,掌握双曲线的方程与性质是解决问题的基础,也是关键,属于基础题.
 ,而双曲线与椭圆
,而双曲线与椭圆 共焦点,
共焦点,∴双曲线的焦点为F(±4,0),又它们的离心率之和为
 ,设该双曲线的离心率为e,则e+
,设该双曲线的离心率为e,则e+ =
= ,
,∴e=2,即
 =2,而c=4,
=2,而c=4,∴a=2,b=2
 .
.∴双曲线方程为:
 -
-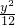 =1;
=1;(2)∵双曲线方程为:
 -
-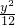 =1,
=1,∴其渐近线方程为y=±
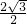 x,
x,即y=
 x或y=-
x或y=- x.
x.分析:(1)由题意可知双曲线的焦点在x轴,并求得焦点为F(±4,0),离心率为2,从而c=4,a=2,b=2
 ;
;(2)利用双曲线方程即可写出其渐近线方程.
点评:本题考查双曲线的标准方程与双曲线的简单性质,掌握双曲线的方程与性质是解决问题的基础,也是关键,属于基础题.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 共焦点,且以
共焦点,且以 为渐近线,求双曲线方程.
为渐近线,求双曲线方程. 共焦点,且以
共焦点,且以 为渐近线,求双曲线方程
为渐近线,求双曲线方程 共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线的标准方程。
,求双曲线的标准方程。 与圆
与圆 的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.
的交点, 且顶点在原点,坐标轴为对称轴,求抛物线的方程.  共焦点,它们的离心率之和为
共焦点,它们的离心率之和为 ,求双曲线方程.
,求双曲线方程.