Question

【题目】等腰直角三角形ABO内接于抛物线y2＝2px(p>0)，O为抛物线的顶点，OA⊥OB，则△ABO的面积是(　　)

A.8p2B.4p2

C.2p2D.p2

Answer 1

【答案】B

【解析】

设等腰直角三角形OAB的顶点A（x1，y1），B（x2，y2），利用OA=OB可求得x1=x2，进而可求得AB=4p，从而可得S△OAB．

设等腰直角三角形OAB的顶点A（x1，y1），B（x2，y2），则=2px1，=2px2，

由OA=OB得：+=+，

∴﹣+2px1﹣2px2=0，即（x1﹣x2）（x1+x2+2p）=0，

∵x1＞0，x2＞0，2p＞0，

∴x1=x2，即A，B关于x轴对称．

∴直线OA的方程为：y=xtan45°=x，由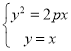解得或，

故AB=4p，

∴S△OAB=×2p×4p=4p2．

故选B