题目内容
已知数列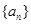 的首项
的首项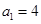 ,且
,且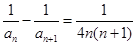 (
( N*),数列
N*),数列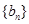 的前
的前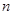 项和
项和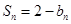 。
。
(1)求数列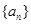 和
和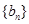 的通项公式;
的通项公式;
(2)设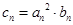 ,证明:当且仅当
,证明:当且仅当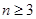 时,
时, 。
。
(1) ;
;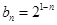
(2)通过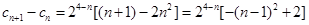 ,当且仅当
,当且仅当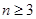 时,
时,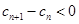 ,即
,即 。
。
解析试题分析:(1)解:∵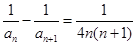
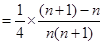
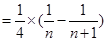
∴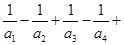 …
…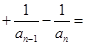
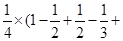 …
…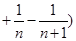
即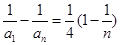
∵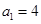
∴
∵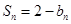
∴当 时,
时,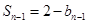
∴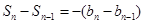
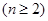
即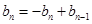
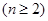
∴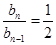
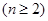
∴数列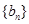 是等比数列,公比为
是等比数列,公比为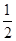 。
。
∵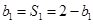
∴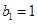
∴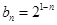
(2)证明:∵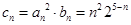
∴
当且仅当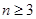 时,
时,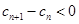 ,即
,即 。
。
考点:本题主要考查等差数列、等比数列的基础知识,“裂项相消法”。
点评:中档题,利用已知条件,布列方程组,先求出数列的通项,从而根据数列通项的特点选择合适的求和方法。“分组求和法”“裂项相消法” “错位相减法”是常常考到的求和方法。

练习册系列答案
相关题目
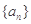 的前n项和为构成数列
的前n项和为构成数列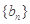 ,数列
,数列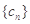 .
.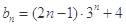 ,则
,则 的图像上一点,数列
的图像上一点,数列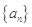 的前n项和
的前n项和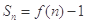 .
. 的前
的前 项和为
项和为 ,
,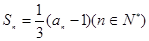
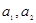 ;
;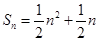
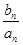 ,求数列
,求数列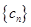 的通项公式
的通项公式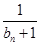 +
+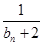 +…+
+…+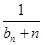 >
>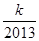 对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由.
对任意正整数n均成立?若存在,求出k的最大值,若不存在,说明理由. 的各项都是正数,且满足:
的各项都是正数,且满足: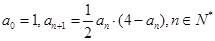
 ;
;
 中,角
中,角 、
、 、
、 成等差数列,且
成等差数列,且 .
.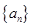 满足
满足 ,前
,前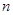 项为和
项为和 ,若
,若 ,求
,求 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
. ,求数列
,求数列 的前
的前 .
. 
