题目内容
已知数列 的各项均为正数,
的各项均为正数, 为其前
为其前 项和,且对任意的
项和,且对任意的 ,有
,有 .
.
(1)求数列 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列 的前
的前 项和
项和 .
.
(1) (2)
(2)
解析试题分析:(1)由已知得 ,
,
∴当 时,
时, ;
;
∴ ,即
,即 ,
,
∴当 时,
时, ;
;
∴数列 为等比数列,且公比
为等比数列,且公比 ; ……4分
; ……4分
又当 时,
时, ,即
,即 ,∴
,∴ ;
;
∴ . ……8分
. ……8分
(2)∵ ,
,
∴ , ……10分
, ……10分
∴ 的前
的前 项和
项和 . ……12分
. ……12分
考点:本小题主要考查等比数列的判定和应用以及裂项法求和.
点评:判定等差数列或等比数列时,不要忘记验证 是否符合;裂项法是求和的主要方法之一,要正确裂项,准确计算.
是否符合;裂项法是求和的主要方法之一,要正确裂项,准确计算.

练习册系列答案
相关题目
已知首项为正数的等差数列{an}的前n项和为Sn,若a1 006和a1 007是方程x2-2 012x-2 011=0的两根,则使Sn>0成立的正整数n的最大值是( ).
| A.1006 | B.1007 | C.2011 | D.2012 |
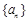 中,
中, ,
,
 且
且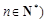 .
. ,
,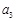 的值;
的值; 是等比数列,并求
是等比数列,并求 项和
项和 .
.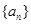 的首项
的首项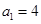 ,且
,且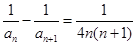 (
( N*),数列
N*),数列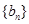 的前
的前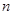 项和
项和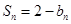 。
。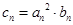 ,证明:当且仅当
,证明:当且仅当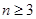 时,
时, 。
。 的三边长
的三边长 ,满足
,满足
 之间插入2011个数,使这2013个数构成以
之间插入2011个数,使这2013个数构成以 为首项的等差数列
为首项的等差数列 ,且它们的和为
,且它们的和为 ,求的最小值;
,求的最小值; ,且
,且 ,求满足不等式
,求满足不等式 的所有
的所有 的值;
的值; 满足
满足 ,证明:数列
,证明:数列 中的任意连续三项为边长均可以构成直角三角形,且
中的任意连续三项为边长均可以构成直角三角形,且 是正整数.
是正整数.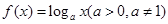 ,已知数列
,已知数列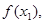
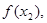
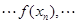 是公差为2的等差数列,且
是公差为2的等差数列,且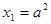 .
.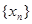 的通项公式;
的通项公式;  时,求数列
时,求数列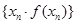 的前
的前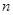 项和
项和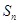 .
. 的前
的前 项和为
项和为 ,且
,且  N
N .
. 是三个互不相等的正整数,且
是三个互不相等的正整数,且 是否成等比数列?并说明理由.
是否成等比数列?并说明理由.  中,
中, 为常数,
为常数, ,且
,且 成公比不等
成公比不等 的值;
的值; ,求数列
,求数列 的前
的前 项和
项和
 }的公差
}的公差 ,它的前n项和为
,它的前n项和为 ,若
,若 ,且
,且 成等比数列,
成等比数列, }的前n项和为
}的前n项和为 ,求证:
,求证: 。
。