题目内容
6.在平面直角坐标系中,O为坐标原点,已知A(-2,0),B(0,-2),C(cosφ,sinφ),其中0<φ<π.(Ⅰ)若$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\frac{5}{3}$,求sin2φ的值;
(Ⅱ)若|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{3}$,求$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角θ.
分析 (I)$\overrightarrow{AC}$=(cosφ+2,sinφ),$\overrightarrow{BC}$=(cosφ,sinφ+2),利用$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\frac{5}{3}$,可得cosφ+sinφ=$\frac{1}{3}$,两边平方即可得出.
(II)由|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{3}$,可得$\sqrt{(cosφ-2)^{2}+si{n}^{2}φ}$=$\sqrt{3}$,化为:cosφ=$\frac{1}{2}$,0<φ<π.解答φ.利用cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}$,即可得出.
解答 解:(I)$\overrightarrow{AC}$=(cosφ+2,sinφ),$\overrightarrow{BC}$=(cosφ,sinφ+2),$\overrightarrow{AC}$•$\overrightarrow{BC}$=$\frac{5}{3}$,
∴cosφ(cosφ+2)+sinφ(sinφ+2)=$\frac{5}{3}$,
∴cosφ+sinφ=$\frac{1}{3}$,
两边平方可得:sin2φ=-$\frac{8}{9}$.
(II)∵|$\overrightarrow{OA}$+$\overrightarrow{OC}$|=$\sqrt{3}$,∴$\sqrt{(cosφ-2)^{2}+si{n}^{2}φ}$=$\sqrt{3}$,化为:cosφ=$\frac{1}{2}$,∵0<φ<π.
∴φ=$\frac{π}{3}$.
∴C$(\frac{1}{2},\frac{\sqrt{3}}{2})$.
∴cosθ=$\frac{\overrightarrow{OB}•\overrightarrow{OC}}{|\overrightarrow{OB}||\overrightarrow{OC}|}$=$\frac{-\sqrt{3}}{2×1}$=-$\frac{\sqrt{3}}{2}$,
∴θ=$\frac{5π}{6}$.
即$\overrightarrow{OB}$与$\overrightarrow{OC}$的夹角为$\frac{5π}{6}$.
点评 本题考查了数量积运算性质、向量夹角公式、三角函数求值,考查了推理能力与计算能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案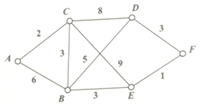 某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )
某市A,B,C,D,E,F六个城区欲架设光缆,如图所示,两点之间的线段及线段上的相应数字分别对应城区可以架设光缆及所需光缆的长度,如果任意两个城市之间均匀光缆相通,则所需光缆的总长度的最小值是( )| A. | 10 | B. | 12 | C. | 14 | D. | 15 |
女性和男性消费情况如表
| 消费金额 | (0,200) | [200,400) | [400,600) | [600,800) | [800,1000] |
| 女性人数 | 5 | 10 | 15 | 47 | x |
| 男性人数 | 2 | 3 | 10 | y | 2 |
| 女性 | 男性 | 总计 | |
| 网购达人 | |||
| 非网购达人 | |||
| 总计 |
| P(Χ2>k0) | 0.10 | 0.05 | 0.010 | 0.005 |
| k0 | 2.706 | 3.841 | 6.635 | 7.879 |
| A. | $\frac{1}{n(n-1)}$ | B. | $\frac{1}{n(n+1)}$ | C. | $\frac{2}{{{{(n+1)}^2}}}$ | D. | $\frac{3}{(n+1)(n+2)}$ |
| A. | (-∞,0) | B. | (-∞,2) | C. | (0,+∞) | D. | (2,+∞) |
 如图,直三棱柱ABC-A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.
如图,直三棱柱ABC-A1B1C1中,CA=CB,M,N,P分别为AB,A1C1,BC的中点.