题目内容
若某几何体的三视图(单位:cm)如图所示,(1)求该几何体体积;
(2)求该几何体表面积.
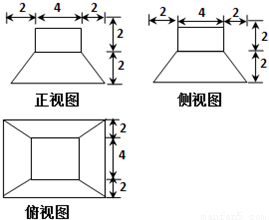
【答案】分析:该几何体为组合体,下面是正四棱台,上底面边长为4cm,下底面边长为8cm,高为2cm,上面是长方体,底面是正方形,边长为4cm,高为2cm,利用体积、面积公式即可得到结论.
解答:解:由题意,该几何体为组合体,下面是正四棱台,上底面边长为4cm,下底面边长为8cm,高为2cm,上面是长方体,底面是正方形,边长为4cm,高为2cm,
(1)该几何体体积为4×4×2+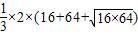 =
=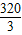 cm3;
cm3;
(2)该几何体表面积为42+82+4×4×2+4×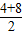 ×2
×2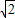 =112+48
=112+48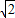 cm2.
cm2.
点评:根据三视图判断空间几何体的形状,进而求几何的表(侧/底)面积或体积,是高考必考内容,处理的关键是准确判断空间几何体的形状.
解答:解:由题意,该几何体为组合体,下面是正四棱台,上底面边长为4cm,下底面边长为8cm,高为2cm,上面是长方体,底面是正方形,边长为4cm,高为2cm,
(1)该几何体体积为4×4×2+
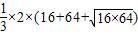 =
=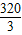 cm3;
cm3;(2)该几何体表面积为42+82+4×4×2+4×
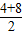 ×2
×2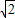 =112+48
=112+48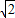 cm2.
cm2.点评:根据三视图判断空间几何体的形状,进而求几何的表(侧/底)面积或体积,是高考必考内容,处理的关键是准确判断空间几何体的形状.

练习册系列答案
相关题目
若某几何体的三视图如图所示,则此几何体的体积是( )


A、
| ||
B、
| ||
C、
| ||
D、
|

 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是
若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是